Seja
a) Determine os pontos críticos de e classifique-os.
b) Determine os pontos de máximo e de mínimo de sobre a região triangular de vértices e .
Passo 1
a) O que o enunciado está pedindo é para gente classificar os pontos críticos dessa função. Para ser ponto crítico, precisa zerar as derivadas ao mesmo tempo:
Vamos encontrar para que pontos isso acontece. Calculando as derivadas:
Descobrindo onde elas zeram ao mesmo tempo:
Aí a gente fica com esse sisteminha para resolver:
Passo 2
Da primeira equação, a gente pode escrever
Daí a gente tem que ou . Vamos olhar cada caso
-
Substituindo na segunda equação
Daí a gente tem dois pontos:
-
Substituindo na segunda equação
Daí a gente tem dois novos pontos:
Aí achamos quadro pontos críticos:
Passo 3
Para classificar esses pontos, a gente precisa calcular o determinante 𝐻(𝑃0):
Se ele for positivo, nosso ponto é de máximo ou de mínimo. Aí se for de mínimo e se for de máximo . Maaas se for negativo, nosso ponto é ponto de sela. (Se for não se sabe).
Vamos calcular então essas derivadas de segunda ordem:
Passo 4
Agora é calcular esse determinante para os nossos pontinhos! Vamos calcular :
Como , e esse é um ponto de mínimo.
Vamos calcular :
Como , esse é um ponto de sela.
Vamos calcular :
Como , esse é um ponto de sela.
Vamos calcular :
Como , esse é um ponto de sela também.
Passo 5
b) Nessas questões onde temos que encontrar os valor máximo e mínimo de uma função dentro de uma região, precisamos fazer duas coisas:
Primeira: Encontrar candidatos a pontos de máximo e mínimo dentro da região dada.
Segunda: Encontrar candidatos na fronteira da região.
E comparar esses candidatos, para ver quem é o valor mínimo e o valor máximo da função. Veeem comigo!
Passo 6
Para encontrar os nossos candidatos dentro da região, precisamos analisar os pontos críticos da nossa função. Já achamos esses pontos:
Precisamos ver se eles estão dentro da nossa região triangular, vamos esboçar ela:
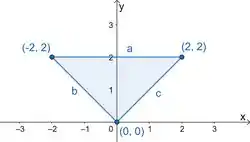
Vamos ver se nossos pontos estão dentro dela:
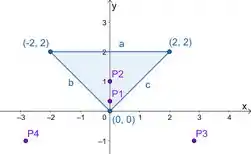
Como só e estão dentro do triângulo, eles serão nossos primeiros candidatos.
Passo 7
Agora precisamos olhar a fronteira. Já vimos que ela tem essa carinha:
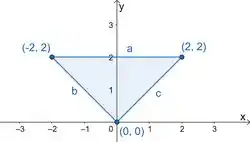
Primeira coisa que a gente faz é automaticamente chamar de candidatos os vértices dessa região:
Passo 8
Agora é achar candidatos nos lados da nossa região. Mas como?? Vamos olhar um de cada vez.
- Lado a: Nele e . Se a gente substitui isso em
Vira uma função de uma variável. Nossos canditatos desse lado vão ser os pontos críticos dessa função. A gente calcula eles assim:
Como , nosso candidato nesse lado vai ser .
- Lado b: Ele é parte da reta e . Se a gente substitui isso em em :, ou seja, chama de :
Vira uma função de uma variável. Nossos canditatos desse lado vão ser os pontos críticos dessa função. A gente calcula eles assim:
Como , e nosso candidato nesse lado vai ser .
- Lado c: Ele é parte da reta e . Se a gente substitui isso em em :, ou seja, chama de :
Vira uma função de uma variável. Nossos canditatos desse lado vão ser os pontos críticos dessa função. A gente calcula eles assim:
Como , e nosso candidato nesse lado vai ser .
Passo 9
Calma que tá acabando haha. Agora é só testar nossos candidatos em e descobrir qual deles dá o maior valor de e qual deles dá o menor:
Daí a gente tira que o valor máximo que essa função nessa região assume é , e ele ocorre em e o valor mínimo é , ele ocorre em .
Resposta
a)
, ponto de mínimo.
, ponto de sela.
, pontos de sela.
b)
, pontos de máximo
, ponto de mínimo