Questão discursiva – UFCG – Calculo diferencial e integral I – Lista 9 – teste – Lista UAMat – Lista 2 – derivadas – questão 14 item g
Derive:
g)
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
A questão nos pede para calcularmos a derivada de uma tal função. Como fazer isso? Bom, que tal vermos a definição. Mas antes, o que é a derivada?
Imagine que temos:
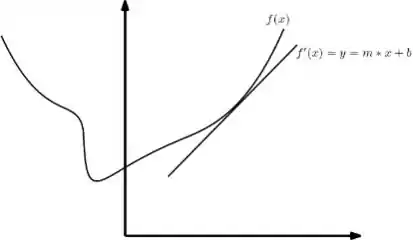
Imagine que temos uma função qualquer e temos então sua reta tangente num ponto qualquer. Mas essa reta tangente realmente toca num só ponto? Podemos provar isso? Por exemplo ela toca em mas não em ? Podemos dizer que não, certo? Então uma visão de perto da reta no ponto:
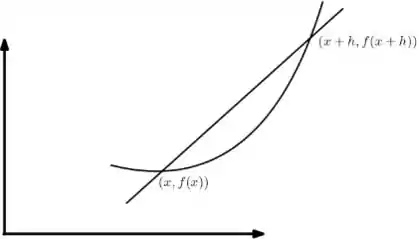
Onde é um passo instantemente depois.
Da reta tangente, sabemos que:
Ou o famoso “ioiô-m-xoxo” que tanto aprendemos. Assim:
Que é:
Mas como garantiremos que qualquer derivada seja exatamente num ponto? Teremos que fazer que o passo seja muito pequeno. Logo vamos tomá-lo indo para , ou seja, tendendo a . Assim:
E este é, portanto, a definição de derivada!! Portanto se queremos saber a derivada da função num ponto, basta aplicarmos essa definição de derivada da função no ponto e analisarmos seus limites.
Então vamos lá?!
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Temos então:
Temos dado que , logo . Assim:
Sabemos que . De forma que:
Sabendo que a soma dos limites é o limite da soma, podemos fazer:
E agora sim podemos fazer ambos os limites separadamente e finalmente acharmos a nossa derivada. Vamos lá?!
Passo 3
Para o primeiro:
Veja que se fizermos , ou seja no ponto, teremos uma indeterminação:
Então podemos aplicar uma sacada genial dos limites: A regra de l’hospital!! Ele é usado quando termos indeterminações num limite. Então derivando em cima e embaixo:
E sobre a derivada do cosseno nós já estamos craques, sabemos que a derivada do cosseno em relação ao é . Assim:
Assim temos que
Agora sim se temos
E achamos o resultado do nosso primeiro limite. Vamos para o segundo?
Para o segundo:
Novamente, veja que se fizermos dará uma indeterminação
E quando temos uma indeterminação significa que novamente podemos usar a regra de l’hospital
mas calma, calma... Veja que é constante para , ou seja, não depende de . E sabemos que a derivada é variação, e se não varia, significa que a derivada é nula. Concluindo:
E, portanto:
E achamos o valor do nosso segundo limite.
Agora vamos descobrir como é a nossa derivada?
MAS ANTES... Você pode estar se perguntando: “Por que essa regra de l’hospital é verdade?” A Regra de L’hopital simplesmente nos diz que o limite de um quociente é igual ao limite do quociente de suas derivadas, desde que as hipóteses do teorema sejam satisfeitas, que é a indeterminação. Aliás, isso que fizemos na demonstração do passo 1 quando falamos da definição de limite. Nós não sabemos o valor de uma função no ponto, mas que sua derivada está lá. E se no ponto é indeterminado, se a derivada no ponto existir então a função existe no ponto. Sacou?
Passo 4
Então tínhamos:
Descobrimos que:
Logo concluímos que:
E achamos, portanto, a derivada de
E terminamos por aqui. Camarada. Obrigado por ter vindo até aqui comigo. Até a próxima!