UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 2.7
Relembre a derivada das funções trigonométricas.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para relembrarmos as derivadas das funções trigonométricas.
Lembra quais são as funções?
Bom, trata-se das seguintes funções: seno, cosseno, tangente, cotangente, secante e cossecante.
Se tiver difícil assim, então dá uma olhada nessa figurinha pra ficar melhor de lembrar:
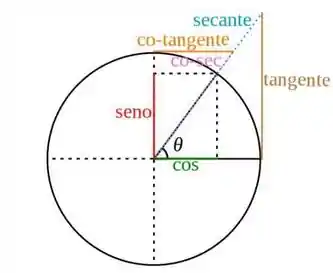
Agora vamos relembrar as derivadas!!
😉
Passo 2
- Derivada do seno é o cosseno:
- Derivada do cosseno é o oposto do seno:
- Derivada da tangente é o quadrado da secante:
- Derivada da cotangente é o oposto do quadrado da cossecante:
- Derivada da secante é o produto da secante e da tangente:
- Derivada da cossecante é o produto da cossecante e da cotangente:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
O semicírculo com diâmetro P Q está sobre um triangulo isósceles P Q R para formar uma região com um formato de sorvete, conforme mostra a figura. Se A ( θ ) for a área do semicírculo e B ( θ ) a área
Em cada item, determine onde f é diferenciável.f (x) = cos sec x
(d) Use a Fórmula (3) para obter (8).
Deduza a Fórmula (4) usando a definição de uma derivada.
Em cada item, determine onde f é diferenciável.f (x) = c o t g x