UFES, Cálculo I, P2, 2020.2, questão 6e
Considere a função cuja derivada é
(e) os pontos de mínimo local de
Passo 1
Faaaala, galeraaaa! Tudo belezinha?
Bom, para descobrir o ponto de mínimo local, basta seguir alguns passos. Devemos:
- Encontrar a derivada primeira;
- Obter os pontos críticos, ou seja, onde ;
- Encontrar a derivada segunda;
- Por fim, sabendo quais são os pontos críticos, devemos analisar se:
- Concavidade para cima: ponto de mínimo;
- Concavidade para baixo: ponto de máximo.
Sabemos que a derivada primeira é
Calculando a derivada segunda, pela regra da cadeia, temos
Assim, podemos reescrever
Calculando a inequação, temos
Separando para analisar a expressão
Observe que sempre será maior que zero, para qualquer valor pertencente aos reais.
Resolvendo a equação do segundo grau
Passo 2
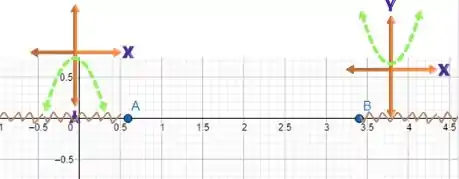
Por fim, podemos desenhar o intervalo em que a concavidade da função é para cima, para que possamos encontrar o ponto de mínimo. Como mostra a figura abaixo.
Logo, quando
Portanto
Prontinho, até mais!
Resposta
Exercícios de Livros Relacionados
O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)