4. Seja
a) Encontre os intervalos onde é crescente ou decrescente;
b) Determine os pontos de e classifique-os como sendo pontos de máximo, de mínimo ou nem de máximo, nem de mínimo (se existirem);
c) Determine os intervalos onde é côncova para cma e côncava para baixo e os seus pontos de inflexão;
d) Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens anteriores.
Passo 1
a) Olá, pessoal! Tudo bom? Aqui temos a seguinte função
E precisamos encontrar os intervalos onde a função é crescente e decrescente. Para isso, vamos analisar a sua derivada,
Precisamos descobrir em quais pontos a derivada é zero
Resolvendo a equação do segundo grau, temos que
Agora vamos ver quando a derivada é positiva, ou seja, função está crescendo; e quando ela é negativa, ou seja, função está decrescendo.

Ou seja, a função é decrescente em e ; e crescente em .
Passo 2
b) Na letra temos que indicar os pontos de máximo e mínimo. Para isso, vamos usar a tabelinha montada no item A. Lá encontramos dois pontos críticos
Para o ponto , temos que a função decresce para valores menores que e depois voltar a crescer, ou seja, temos um ponto de mínimo.
Já no ponto , temos que a função cresce para valores menores que e depois volta a cair, ou seja, temos um ponto de máximo.
Passo 3
c) Para análise da concavidade, vamos olhar para a segunde derivada,
Igualando a zero, ficamos com
Analisando a função ficamos com
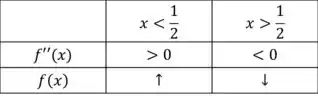
Pelo Teste da Concavidade, temos que é côncava para cima para valores menores que e côncava para baixo para valores maiores que .
Os pontos de inflexão são pontos onde a concavidade muda. Logo, é o único ponto de inflexão de .
Passo 4
d) Juntando todas essas informações, podemos esboçar o seguinte gráfico
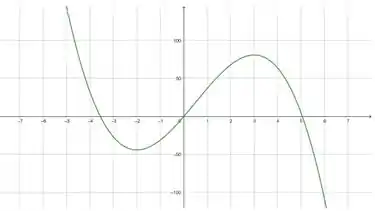
Resposta
No texto.