Sendo:
Encontre os intervalos onde a função é crescente e decrescente.
Em seguida, identifique os valores extremos locais da função, se houve, informando onde ela os assume.
Alguns desses valores extremos são absolutos? Quais?
Passo 1
Para encontrar onde a função cresce ou decresce, devemos encontrar as raízes da derivada ou determinar quando ela não existe e testar valores à esquerda e à direita desses pontos. Resumindo, aplicamos o teste CD.
Para tal, vamos derivar. Usando a regra do produto:
Passo 2
As raízes vão ser determinadas pelos numeradores:
E não vai existir para quando:
Passo 3
Agora, vamos testar valores à esquerda e à direita:
Para , podemos escolher e :
Então a derivada é negativa à esquerda e positiva à direta de .
Para , podemos escolher e :
Então a derivada é positiva à esquerda e negativa à direta de .
Para , não há valores à esquerda, pois a derivada terá raiz negativa no denominador. Para valores à esquerda, já sabemos, pois:
Para , não há também valores à direita, pelo mesmo motivo de cima. Para valores à esquerda, sabemos que:
Com todas essas informações. Temos que:
Função crescente para .
Função decrescente para .
Passo 4
Para acharmos máximos e mínimos, determinamos os pontos críticos que serão as raízes da derivada ou quando ela não existe. Já determinamos isso aí. Serão os pontos:
Já também testamos os sinais à esquerda e à direita de cada ponto, que é o teste da primeira derivada.
A derivada é negativa à esquerda e positiva à direta de . Então temos um ponto de mínimo aqui.
A derivada é positiva à esquerda e negativa à direta de . Então temos um ponto de máximo aqui.
A derivada é negativa à direta de e não existe à esquerda
A derivada é negativa à esquerda de e não existe à direita.
Vai ficar assim:
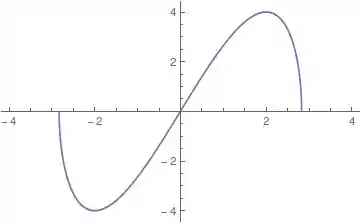
Passo 5
Agora precisamos saber se são extremos locais ou absolutos. O ponto de máximo é:
Para :
Para as fronteiras da função:
:
:
O ponto é um ponto de máximo que é maior que os valores na fronteira. Então é um ponto de máximo global.
Se houvesse outros pontos de máximo, também deveria ser maior que estes para ser máximo global.
Para o ponto de mínimo:
Para :
O ponto é um ponto de mínimo que é menor que os valores na fronteira. Então é um ponto de mínimo global.
Se houvesse outros pontos de mínimo, também deveria ser menor que estes para ser mínimo global.
Resposta
Função crescente para .
Função decrescente para .
A derivada é negativa à esquerda e positiva à direta de . Então temos um ponto de mínimo aqui.
A derivada é positiva à esquerda e negativa à direta de . Então temos um ponto de máximo aqui.
é ponto de máximo global. é mínimo global.