UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 3b.
-
Seja a função , determine:
- Os intervalos onde a função é crescente e onde ela é decrescente e os pontos de máximo e mínimo relativos da função:
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão dá pra gente a função
e pede para gente dizer quais os intervalos onde a função é crescente e onde ela é decrescente e os pontos de máximo e mínimo relativos da função. Então nós vamos dividir essa questão em duas parte de uma forma que ajude a gente a achar tudo que está sendo pedido.
Primeiro vamos achar os pontos críticos da função, e depois fazermos o estudo do sinal da derivada para determinar os pontos de máximo e mínimo relativos e os intervalos de crescimento e decrescimento da função.
Vem comigo que vamos fazer isso juntos.
Passo 2
A primeira coisa que devemos fazer é encontrar os pontos críticos, e para isso devemos lembrar que temos pontos críticos nos locais onde a derivada da nossa função vai a zero. Assim faremos:
E derivando ficamos com:
Agora vamos igualar a derivada a zero e resolver a equação encontrada
Para resolver essa equação, podemos colocar o em evidência, ficando com:
Como temos um produto dando zero, um dos dois fatores deve ser igual a zero, assim nossos pontos críticos serão:
E
Maravilha, agora precisamos saber quais os pontos de máximo e mínimo e os intervalos de crescimento e decrescimento, e para isso faremos a análise de sinal da derivada no próximo passo.
Passo 3
Acabamos de encontrar os pontos críticos, então vamos dividir nossos intervalos da seguinte forma:
Precisamos investigar qual o sinal da derivada para valores menores que , para valores entre e e para valores maiores que
Para valores menores que .
Podemos substituir diretamente um valor menor que na derivada da nossa função, como por exemplo o . Veja:
Então chegamos à conclusão que para valores menores que a derivada da função é negativa, indicando que nesse intervalo a função é decrescente. E escrevemos que
Para valores maiores que e menores que. :
Podemos pegar o :
Então chegamos à conclusão que para valores maiores que e menores que a derivada da função é positiva, indicando que nesse intervalo a função é crescente. E escrevemos que
Para valores maiores que. :
Podemos pegar o
Então chegamos à conclusão que para valores maiores que a derivada da função é negativa, indicando que nesse intervalo a função é decrescente. E escrevemos que
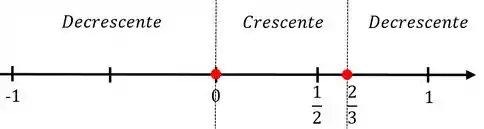
Com essa análise de sinal também somos capazes de classificar nossos pontos críticos localmente. É o que faremos no próximo passo.
Passo 4
Veja o que está acontecendo em torno do ponto , a função é decrescente antes dele e crescente depois dele, isso nos diz que esse é um ponto de mínimo local.
Já para temos que a função é crescente antes dele e decrescente depois, indicando que esse é um ponto de máximo local.
Assim:
é ponto de mínimo local
E
é ponto de máximo local
E pra confirmar tudo isso que calculamos, aí vai o gráfico da nossa função:
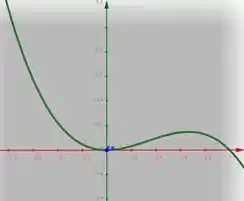
E prontinho. Problema resolvido. 😊
Partiu próxima?!