Deseja-se construir uma piscina retangular com de área (da superfície) a de distância de um muro. Paralela aos demais lados da piscina será construída uma cerca, deixando um corredor de circulação de de largura.
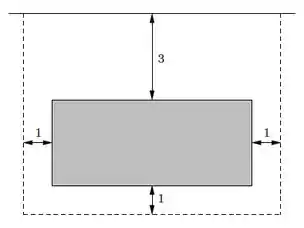
Sabe-se que os lados da piscina paralelos ao muro devem ter no mínimo e no máximo . Sejam e as áreas mínima e máxima que a região cercada pode ter. Então, vale:
Passo 1
Vamos chamar o comprimento da piscina de e a altura de . Sendo assim, a região cercada é dada por
Essa é a função para a qual precisamos encontrar um valor máximo e um valor mínimo. Então teremos que derivar, mas antes precisamos escrever a área em função de apenas uma variável. Já que o enunciado diz que
e sabemos que
então podemos isolar uma dessas variáveis e depois substituir na função da área.
E finalmente
Passo 2
Agora vamos derivar a função encontrada para a área e encontrar seus pontos de máximo e de mínimo.
O valor negativo foi desconsiderado, pois estamos lidando com medidas.
Encontramos o ponto critico e fazendo o teste da primeira derivada teremos o seguinte
para
para
Logo, é ponto de mínimo da função.
Passo 3
Quando entao e a área será mínima , valendo:
Se invertermos os valores, isto é, e a área será máxima :
Portanto, vale
Resposta
d)