UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 1f.
- Defina:
- Mínimo relativo e mínimo absoluto de uma função.
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão pede para definir o que é o mínimo relativo e o mínimo absoluto de uma função. Correto?
E o que podemos perceber pela é que existe uma diferença entre eles. Já que o problema pede para que a gente defina os dois.
Então vamos começar por partes aqui. Vamos primeiro entender o que significa o mínimo de uma função, e depois a gente diferencia o mínimo relativo do mínimo absoluto. Beleza?!
Vem comigo que te ajudo com isso.
Passo 2
Um ponto de mínimo é um ponto na função que é menor que os pontos próximos a ele. Em um gráfico, é como se tivéssemos vale:
Se a gente olhar com calma, vamos perceber nesses pontos de mínimo a reta tangente à função é horizontal, ou seja, o coeficiente angular dela é zero.
E você se lembra que o coeficiente angular da reta tangente à um ponto é justamente a derivada da curva naquele ponto? Então, a gente acabou de chegar à conclusão de que para pontos de mínimo a derivada da curva é nula naquele ponto, ou seja, se em temos um ponto que pode ser de mínimo:
Mas cuidado, porque os pontos de mínimo não são os únicos em que a derivada da função vai a zero. Isso também pode acontecer em pontos de máximo ou pontos de sela.
Então devemos fazer teste para saber se o pondo encontrado ao fazer a derivada igual a zero é mesmo um ponto de mínimo.
Passo 3
Para saber se o ponto é mesmo um ponto de mínimo, podemos fazer o teste da primeira derivada. Que consiste em analisar o sinal das derivadas da função em pontos próximos ao que estamos analisando. Assim, se a derivada em um ponto anterior ao nosso ponto for negativa e a derivada em um ponto posterior for positiva, estamos trabalhando com um ponto de mínimo.
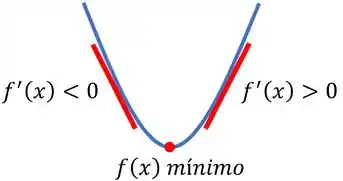
Show, mas agora vamos diferenciar o ponto de mínimo local e mínimo global. Beleza?
Passo 4
Nem sempre que achamos um mínimo da função, esse vai ser exatamente o menor valor que a função pode assumir. Olha só essa função aqui:
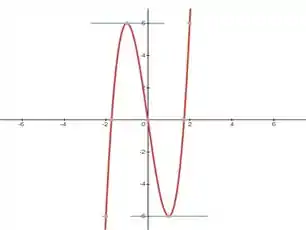
Vemos que para temos um mínimo, mas se olharmos pelo gráfico conseguimos ver que a função pode atingir valores menores, é só pegar um um pouco menor e vamos perceber que o ponto de mínimo não reflete o menor valor que a função pode assumir, né?
Nesses casos, falamos que o ponto que nós achamos, é na verdade ponto de mínimo local. Caso de fato eles sejam os menor valor que a função assuma, nós os chamaremos de mínimo global ou absoluto.
Para determinar se esses caras são globais ou locais, devemos sempre ficar de olho nos extremos da nossa função.
Assim,
E assim respondemos mais uma questão. Bora olhar a próxima!
Resposta
No desenvolvimento.