UTFPR, Londrina, Cálculo 2, Lista Máximos e Mínimos - UTFPR - 2022.2, Questão 1.
Determine os valores de máximo e mínimo da função na placa triangular fechada e limitada pelas retas ; ; no primeiro quadrante.
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nessa questão queremos obter os pontos de máximos e mínimos da função dentro da região limitada por , e .
E aí, como fazemos isso? 👀
Primeiro calculamos os pontos críticos da função e vemos quais estão dentro da região limitada, depois fazemos as mesmas analises para os limites da região, ou seja, em , e .
No caso, a região é dada por
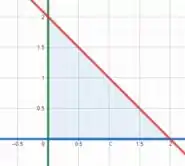
Entendeu?
Passo 2
Para calcular os pontos críticos de , derivamos pelo método de derivação polinomial e igualamos a
Primeiro com relação a
Igualando a
Agora fazemos o mesmo para
Igualando a
Fazendo a combinação dos pontos, vemos que não está no primeiro quadrante,, então não nos interessa.
O que nos resta é obter os pontos críticos nos extremos da região!
Tranquilo até aqui? 😁
Passo 3
Em e , se substituirmos e derivarmos , vamos obter os mesmos valores para os pontos críticos.
Portanto o ponto se encaixa nos nossos requisitos e vamos analisa-lo depois
Substituindo em , temos
Derivando e igualando a ...
é negativo, então também não nos interessa.
Por fim, o que resta são os vértices da região.
, e
Bacana, não é? 😎
Passo 4
Agora vamos testar os pontos , , e e verificar qual possui maior imagem.
Para
Para
Para
E por último,
Com isso, vemos que os pontos e são os pontos máximos e é o ponto mínimo!
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
e são os pontos máximos e é o ponto mínimo