1.
e. Existe uma função contínua em com máximo global em e mínimo global em ?
Passo 1
Oi, galerinha! Tudo bom? Antes de tudo, precisamos entender que ponto é esse!
Um ponto de máximo é um ponto na função que é maior que os pontos próximos a ele. Em um gráfico, é como se tivéssemos o topo de uma colina. Já um ponto de mínimo é justamente o contrario, podemos pensar que ele tem a forma de um buraco.
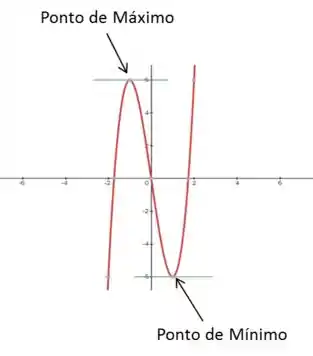
E como sabemos se uma função não terá um máximo ou mínimo?
Repara que no gráfico acima possui uma reta azul, nos pontos de máximo e mínimo, que representa a reta tangente ao ponto. Se a gente olhar com calma, vamos perceber que tanto pra pontos de máximo quanto pra pontos de mínimo a reta tangente à eles é horizontal, ou seja, o coeficiente angular delas é zero.
Lembra que o coeficiente angular da reta tangente a um ponto é justamente a derivada da curva naquele ponto? Opaaa, então a gente acabou de chegar a conclusão de que para pontos de máximo e mínimo, a derivada da curva é nula naquele ponto.
Passo 2
Galerinha, então, respondendo a pergunta fala sobre máximo e mínimo global. Então vamos olhar para essa função aqui:
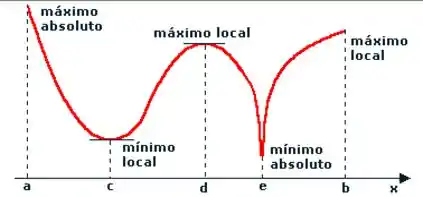
Repara que a função tem vários pontos de máximo e mínimo. Para determinar se esses caras são globais ou locais, devemos sempre ficar de olho nos extremos da nossa função. Repare que, se quiséssemos achar um ponto de máximo ou mínimo, derivando a função e realizando os testes das derivadas, iríamos achar os pontos e , sendo um mínimo e um máximo.
Porém, o ponto NÃO é o ponto de máximo global, mas sim o ponto , no extremo do intervalo analisado. Por isso, é importante testar e (extremos do intervalo) e compará-los com no ponto crítico anteriormente encontrado.
Ou seja, a resposta é sim!
Resposta
Sim