UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.30a
As funções abaixo tem máximos/mínimos locais:
a)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pergunta se a função tem máximo ou mínimo local.
Vamos dar uma analisada rapidinho aqui...
A função é uma função em valor absoluto, também conhecida como função módulo.
Essa função tem um "v" no ponto , onde a concavidade da função muda.
Nesse ponto, ela não possui um máximo ou mínimo local.
Mas mesmo assim, vamos dar uma olhadinha melhor nela??
😉
Passo 2
Para você entender melhor, vamos esboçar o gráfico de :
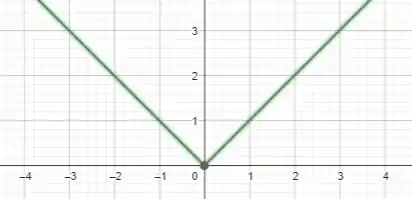
Agora vamos analisar o gráfico para casos:
- ;
- ;
- .
Passo 3
- Para .
- Para .
- Para .
Nessa região, a função é uma reta crescente e não possui nenhum máximo ou mínimo local.
Nessa região, a função é uma reta decrescente e não possui nenhum máximo ou mínimo local.
Nesse ponto, a função atinge o valor mínimo de zero, mas não é considerado um mínimo local, pois a função não é crescente nem decrescente em uma vizinhança de .
Entendeu direitinho? Responde aee ;)
Resposta
A função não tem máximos/mínimos locais