Identifique os pontos de máximo e mínimo e de inflexão da função abaixo.

Os pontos críticos estão localizados onde a derivada não existe ou é zero. Essa derivada é um polinômio, então vai sempre existir. Vamos ver quando ela será zero:

Por Bhaskara:

Da mesma maneira:

Esses serão os pontos críticos da função. Antes de determinar se são pontos de máximo ou mínimo, vamos calcular os pontos de inflexão.

Os pontos de inflexão ocorrem quando a segunda derivada não existe ou é zero. Para isso, derivamos a função novamente:

Por se tratar de um polinômio, a segunda derivada sempre existirá. Será zero quando:

Este será nosso ponto de inflexão.

Voltamos agora aos pontos críticos para determinar qual é máximo e qual é mínimo. Cara, por que você deu volta e não seguiu com isso antes? Porque, ao calcular os pontos de inflexão, nós calculamos a segunda derivada da função. E com a segunda derivada fica muito mais fácil encontrar os pontos de máximo e mínimo.

Só precisamos aplicar o teste da segunda derivada. Nos pontos críticos:

Como a segunda derivada é positiva, trata-se de um ponto de mínimo.

Para o segundo ponto crítico:

Como a segunda derivada é negativa, trata-se de um ponto de máximo.

Toda vez que a gente quer encontrar um ponto de máximo ou mínimo, você deve optar em aplicar o teste da segunda ou da primeira derivada. Quando a segunda derivada é fácil de calcular, foi dada, ou você já vai ter que calculá-la de qualquer forma, opte pelo teste da segunda derivada, que é mais rápido.

Se fossemos aplicar o teste da primeira derivada aqui. Deveríamos escolher um ponto a esquerda e direita do ponto crítico, sem nunca extrapolar um ponto crítico que não é o que gente está tratando.

Para . Podemos escolher e :

Como é negativo à esquerda e positivo à direita, temos, como antes, um ponto de mínimo.

Para . Podemos escolher e

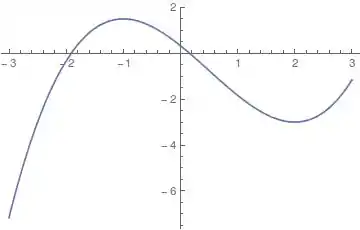
Como é positivo à esquerda e negativo à direita, temos, como antes, um ponto de máximo, como no gráfico: