1ºEE – Cálculo 1 – UFPE – 2022.2 – Questão 2b
2Calcule os seguintes limites (NÃO é permitido o uso da regra de L’Hospital):
b)
Passo 1
Fala meus chuchuzinhos da UFPE, bora matar essa questão de Cálculo 1?
Questão de limite, primeiro passo é substituir o valor e ver no que dá:
Caímos em uma indeterminação , vamos precisar trabalhar com o polinômio de cima e o de baixo da nossa fração, afim de sumir com essa indeterminação.
Como temos uma raíz, vamos usar aqui a técnica de multiplicar pelo conjugado.
Passo 2
Bom, nosso polinômio do numerador é
Vamos então multiplicar nossa fração (tanto em cima quanto em baixo) pelo conjugado desse cara aí que é:
Teremos portanto:
Bom, agora vemos ver se conseguimos sair da indeterminação, substituindo o valor do limite:
Voltamos pra indeterminação do tipo . Mas repara no seguinte, quando substituímos na fração, o termo que zera no numerador é o e o termo que zera no denominador é . Portanto, se dividirmos ambos os termos por , sendo a raíz desses termos, poderemos reescrever a fração e anular o em cima e embaixo, vem comigo!
Passo 3
Dividindo por , teremos:
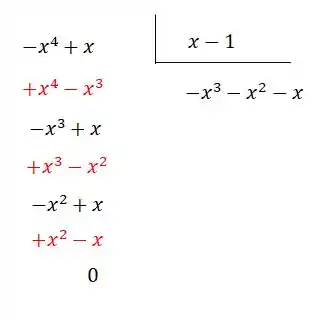
Portanto, podemos reescrever como sendo:
E agora dividindo por , teremos:
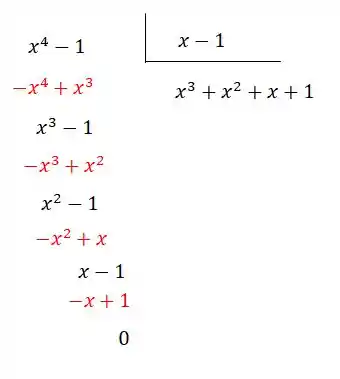
Portanto, pode ser reescrito como:
Substituindo essas expressões que encontramos no nosso limite, teremos:
E portanto, podemos cortar o de cima com o de baixo, e isso deverá acabar com a nossa indeterminação:
Por fim, só devemos substituir o valor do limite, para verificar se chegamos em um valor real: