- Calcule o limite, se existir
f.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos um limite para resolver,
A gente sempre começa substituindo o valor na função, fica assim:
Eitaaa, caímos numa indeterminação do tipo .
Bora sair dessa!
Passo 2
Para sair dessa indeterminação, vamos reescrever essa função! Repara que no numerador podemos reescrever o numerador assim:
Agora vamos aplicar a seguinte relação,
Com isso, temos que
Vamos para o denominador!
Passo 3
Agora temos uma equação do terceiro grau,
E vimos que zera a equação, ou seja, ele é uma raiz. Então vamos dividir nossa equação do terceiro grau por e reesscrevê-la.
Para isso vamos fazer o nosso Briof-Ruffine.
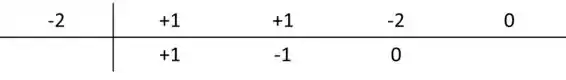
Logo,
Vamos voltar para o nosso limite!
Passo 4
Reescrevendo tudo, ficamos com
Simplificando o , ficamos com
Calculando,
Prontinho!
Resposta
Exercícios de Livros Relacionados
Existe um número a tal que lim x → - 2 3 x 2 + a x + a + 3 x 2 + x - 2 exista? Caso afirmativo, encontre a e o valor do limite.
Calcule o limite, se existir. lim h → 0 ( 3 + h ) - 1 - 3 - 1 h
Calcule o limite, se existir. lim x → 1 x 3 - 1 x 2 - 1
Determine o limite infinito.underset(x - pi^-)(lim) cot x
Calcule o limite, se existir. 12 . lim x → - 4 x 2 + 5 x + 4 x 2 + 3 x - 4