Calcule os limites:
e)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um limite e nos pede para resolvê-lo, certinho?
Mas e aí, como podemos resolver esse limite?
Podemos simplesmente substituir ??? Naaao!!! Pois resultaria uma indeterminação (divisão por zero)!!
Então nos resta fazer algumas manipulações para podermos encontrar!!
Bora junto descobrir!! 😉
Passo 2
Seguinte... para simplificar, vamos pegar a equação do numerador e vamos dividir pela equação do denominador (divisão de polinômios):
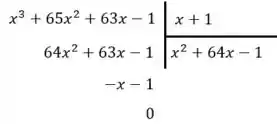
Dessa forma, podemos dizer que:
Agora vamos substituir no nosso limite!!
Passo 3
Agora, aplicando no limite, temos:
Substituindo, temos:
Agora vamos para o próximo!!
Entendeu direitinho? Responde aee ;)
