UFAM, Cálculo I, Lista 4, 2020, questão 1i
Calcule os seguintes limites. Justifique suas respostas.
i)
Passo 1
Faaaaala, galeeeera! Vocês estão prontos para começar?
Nessa questão vamos ter que calcular limites de funções apresentadas no enunciado. Os limites nada mais são que uma forma de analisar o comportamento de uma função à medida em que seu argumento se aproxima de um dado valor. Vamos resolver essa questão?
Bom, primeiramente podemos reescrever o limite. Usando a seguinte propriedade.
Veja só:
Passo 2
Vamos agora calcular cada limite separadamente.
Calculando o primeiro limite. Observe o gráfico dessa função.
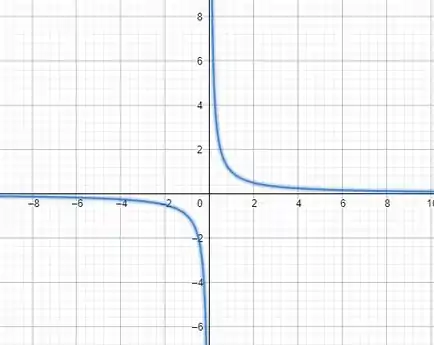
Logo,
Calculando o segundo limite, podemos também verificar o comportamento da função pelo seu gráfico
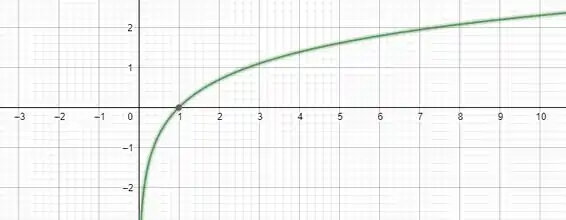
Logo
Passo 3
Por fim, subtraindo os valores, temos
Até a próxima!
Resposta
Exercícios de Livros Relacionados
Existe um número a tal que lim x → - 2 3 x 2 + a x + a + 3 x 2 + x - 2 exista? Caso afirmativo, encontre a e o valor do limite.
Calcule o limite, se existir. lim h → 0 ( 3 + h ) - 1 - 3 - 1 h
Calcule o limite, se existir. lim x → 1 x 3 - 1 x 2 - 1
Determine o limite infinito.underset(x - pi^-)(lim) cot x
Calcule o limite, se existir. 12 . lim x → - 4 x 2 + 5 x + 4 x 2 + 3 x - 4