1ºEE – Cálculo 1 – UFPE – 2022.2 – Questão 2a
2. Calcule os seguintes limites (NÃO é permitido o uso da regra de L’Hospital):
a.
Passo 1
Fala meus chuchuzinhos da UFPE, bora matar essa questão de Cálculo 1?
Questão envolvendo o cálculo de limite em uma divisão de polinômios. Primeira coisa que a gente deve fazer é colocar o valor do limite e ver se dá um valor ou se cai numa indeterminação:
Caímos em uma indeterminação do tipo .
Precisamos portanto reescrever o polinômio de cima e o de baixo para ver se conseguimos anular algum termo afim de sairmos dessa indeterminação.
Como o valor zerou ambos os polinômios, uma boa opção será dividir o polinômio de cima e o de baixo por e então reescreve-los, vamos fazer isso no passo 2.
Passo 2
Bom, nosso polinômio do numerador é
Que é um polinômio de segundo grau, portanto, podemos utilizar Bhaskara e reescreve-lo da seguinte forma:
Onde é o mesmo da fórmula de Bhaskara, ou seja, o valor que acompanha que nesse caso é .
e são as raízes desse polinômio que vamos encontrar usando Bhaskara:
Portanto o polinômio de cima pode ser reescrito como:
Vamos agora reescrever o de baixo que é um polinômio de terceiro grau e não vamos poder usar Bhaskara
Passo 3
O polinômio do denominador é:
Vamos dividir esse polinômio por , que é um bom chute para ser uma das raízes desse polinômio, além disso, poderemos anular que aparecerá em baixo com o que apareceu em cima.
Fazendo a divisão de polinômios teremos:
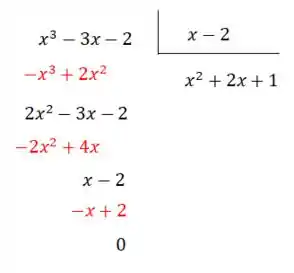
Portanto, podemos reescrever o polinômio do denominador da seguinte forma:
Passo 4
Agora a gente vai substituir o que encontramos nos Passos 2 e 3 na nossa fração:
E como temos em cima e embaixo, podemos corta-lo:
Esse processo deve ter sido suficiente para sumir com a nossa indeterminação, agora é só substituir o valor do limite e ver se chegamos em algum resultado:
E chegamos na nossa resposta!