UFSC – Cálculo 1 – Listas – Listas de Derivadas – Lista 2.10 – Derivadas de Ordem Superior – C5
Considere um sistema massa-mola sem atrito em que a massa do sistema é m e a constante de elasticidade da mola é .
- Coloque a origem do eixo de coordenadas na posição de repouso do sistema e use a segunda lei de Newton e a lei de Hooke para para concluir que
- Assuma posição inicial e velocidade inicial são e , respectivamente, e mostre que essa situação pode ser descrita por encontrar uma função que satisfaz
- Mostre que, para quaisquer números e , a função satisfaz , em que .
- Mostre que, para satisfazer e , então .
- Mostre que .
- Determine para e . Interprete o resultado fisicamente.
- Determine para e . Interprete o resultado fisicamente
Passo 1
Falaee, beleza?? Seguinte.. vamos primeiro fazer uma figura para podermos entender melhor o problema, belezinha? Se liga ae:
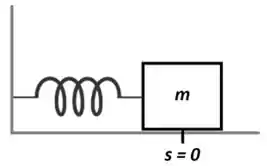
Note que atribuímos a origem do eixo de coordenadas quando o objeto está em repouso (quando ).
Assim, pela 2ª Lei de Newton, sabemos que, para essa posição adotada do objeto:
Pelo diagrama do corpo livre, podemos observar que:
Logo, substituindo os valores, encontramos:
Passo 2
Para a letra (b), a gente tem que saber que sendo e os valores iniciais de posição e velocidades iguais a e respectivamente, temos para a situação:
Passo 3
Para a letra (c) temos que, derivando :
E derivando novamente:
E, substituindo , temos:
Passo 4
Para a letra (d), seja:
Aí a gente deriva de tal forma que:
Assim, substituindo em , temos:
Passo 5
Para a letra (e), se substituirmos e em , temos:
Lembrando que , logo:
Passo 6
Para a letra (f), quando e , temos que .
Tá... mas o que isso significa?
Significa que essa situação reflete o estado de repouso do sistema massa-mola!!!
Passo 7
Na letra (g) temos que para e , .
Tá... outra vez.. o que isso significa???
Essa situação reflete o estado em que a mola foi esticada até o ponto de distância da origem, enquanto indica que a posição da massa do sistema oscilará entre e .
Entendeu direitinho? Responde aee ;)
Resposta
Ei, a resposta está no passo a passo :)