Lista 2.10 – Derivada de ordem superior – UFSC – Cálculo 1 – Questão C4
[Queda livre com resistência do ar.] Considere um objeto de massa m que é largado em queda livre numa situação em que a força de resistência que o ar oferece é diretamente proporcional à velocidade do objeto com constante de proporcionalidade k.
- Coloque a origem do eixo de coordenadas na posição inicial do objeto e com sentido positivo na direção do movimento. Use a segunda lei de Newton para concluir que .
- Mostre que essa situação pode ser descrita por encontrar uma função s(t) que satisfaz
- Mostre que, para quaisquer números A e B, a função satisfaz a equação .
- Mostre que, para satisfazer e , então .
- Mostre que .
Passo 1
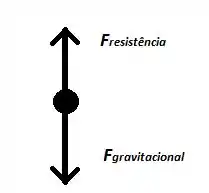
Falaee, beleza?? Seguinte.. vamos primeiro fazer o diagrama do corpo livre para compreendermos melhor o problema:
Passo 2
Sabemos que:
E, pela Lei de Newton, temos que:
Assim, substituindo os valores, temos:
Passo 3
Sabendo que e e que, na origem, e , a equação de (a) pode ser resumida por:
Passo 4
Derivando , temos:
E, fazendo a segunda derivada, temos:
Por outro lado, substituindo na equação, temos:
Como encontramos o mesmo resultado para , o resultado confere.
Passo 5
Seja , sabemos que:
Nesse mesmo sentido, para , temos que:
Como temos , então podemos encontrar :
Dessa forma, substituindo e em , temos:
Passo 6
Ainda, sabe-se que , logo, sendo , temos que:
Entendeu direitinho? Responde aee ;)
