UFSC – Cálculo 1 – Lista 2.6 – Questão P7
Sejam e funções cujos gráficos estão abaixo
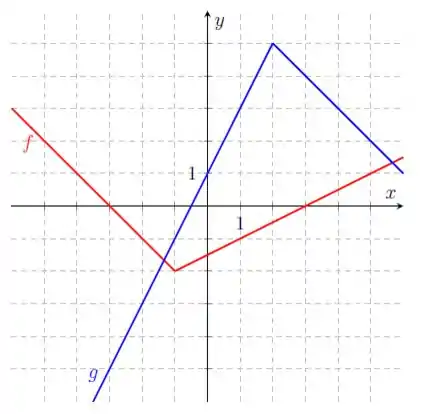
Determine e , em que
Passo 1
E ai galera, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Bora lá?
O enunciado nos deu um gráfico de duas funções: em vermelho e em azul. E nos perguntou as derivadas de uma outra função em três pontos distintos:
Mas o que será que tem a ver essa função com as funções dadas?
A função é definida como o produto das funções e !
Está aqui nosso vínculo!
O problema pediu a derivada de uma função (nossa querida ) que por sua vez é o produto de outras duas funções!
E já sabemos: para determinar a derivada de uma função que é produto de funções tascamos a REGRA DO PRODUTO!
A regra do produto nos diz que a derivada de uma função que é o produto de duas funções é: “derivada da primeira vezes a segunda, mais derivada da segunda vezes a primeira”
Como queremos em três pontos distintos, precisamos aplicar essa regra em três diferentes. Por exemplo, considerando que o é temos
Beleza?
Mas aí você se pergunta... como vou achar esses valores? Aí que entra nosso gráfico!
Notem que ele só envolve retas! Sabe por quê? Porque derivada de reta é constante! É o coeficiente angular da reta!
Isso mesmo! Achar a derivada de uma reta em um ponto, é achar a inclinação dessa reta (nosso conhecido coeficiente angular lá do colégio) em torno desse ponto!
E por quê ser a inclinação?
Isso porque, vamos supor uma reta de equação qualquer
Lá do colégio a gente aprendeu que o “a” é o coeficiente angular e o “b” é o coeficiente linear, certo?
Bom, agora em cálculo você aprendeu a derivar! Então vamos derivar essa função aí:
Lembrando que derivada de constante é zero
Aí
Então a derivada de uma reta qualquer é igual ao coeficiente angular dessa reta nesse ponto!
Eu digo em torno do ponto, porque por exemplo, a reta em vermelho é partida em dois pedaços: até é decrescente e depois passa a ser crescente. Ela é composta por duas leis de função, mas isso não importa para a gente agora! O que importa é encontrarmos o coeficiente angular dessa reta nos pontos que o problema pediu!
E a função no ponto? É o daquele ponto! De novo, é só dar um bizu no gráfico! Mas calma que vou fazer junto com você!
Passo 2
Vamos começar com a derivada do primeiro ponto .
Aí aplicando a regrinha do produto (vou colar lá do passo anterior) aplicado em temos
Precisamos achar quatro valores:
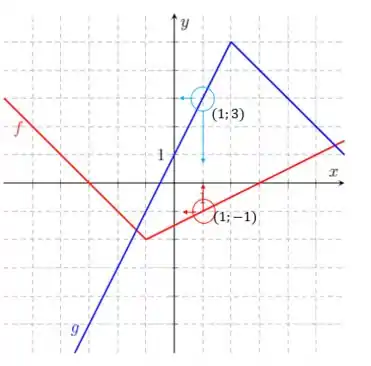
Bom, como comentei, os valores (1) e (2) são as ordenadas de cada função no ponto . Vamos olhar no gráfico:
Em torno da abscissa a função em vermelho assume o valor de , enquanto a função (em azul) assume o valor de .
Assim:
Beleza?
Passo 3
Agora vamos calcular os coeficientes angulares. Calcular coeficiente angular é bem tranquilo, saca só!
A gente precisa de dois pontos do gráfico e e daí é só jogar nessa fórmula aqui:
Vamos ao nosso gráfico de novo, agora olhando para a função vermelho em torno de :
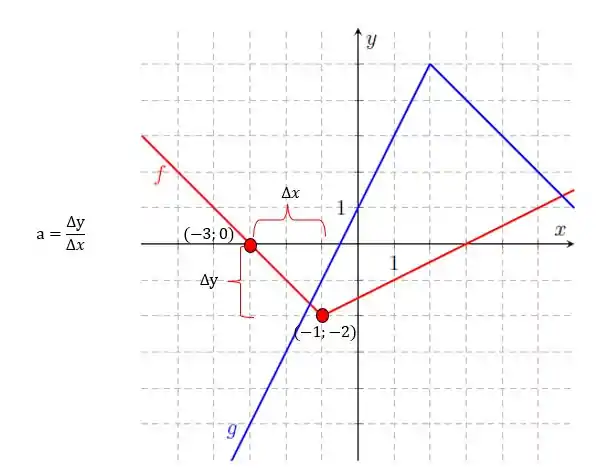
E agora é só calcular :
Assim é:
Beleza?
Agora vamos fazer a mesma coisa para a função em azul.
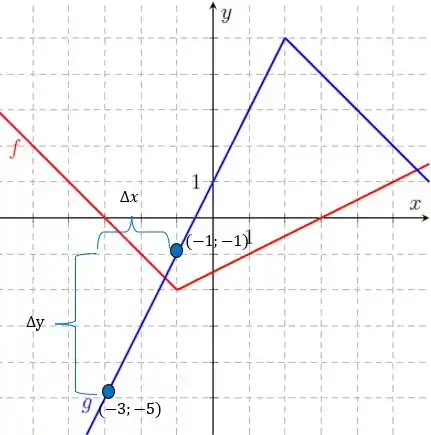
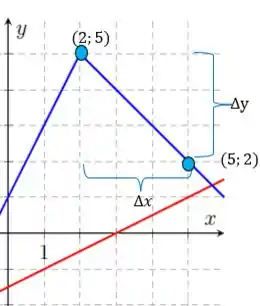
Do gráfico temos que os pontos são e e assim o coeficiente angular da reta em azul é
E a derivada de em é:
Juntando os resultados temos:
Passo 4
Resgatando lá do passo 2 a regra do produto
Os quatro valores:
Agora é aplicar na regra:
Tranquilo? Agora é repetir esse processo para os outros dois pontos e !
Vamos lá! Não desanima!
Passo 5
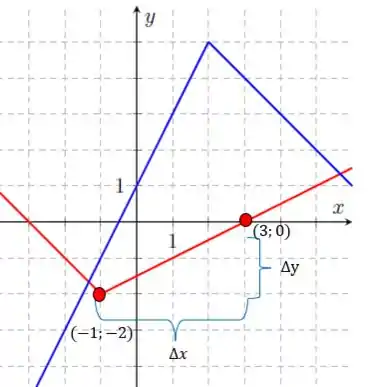
Para os valores de e são:
Os valores são
E agora as derivadas. Primeiro de em vermelho:
A derivada é:
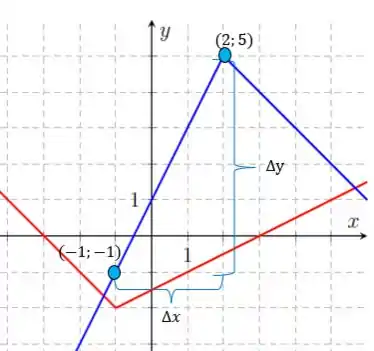
Mas nem precisaríamos fazer essa conta, já que a função tem a mesma inclinação desde o até !
Assim
Passo 6
Os quatro valores:
Agora é aplicar na regra:
Beleza?
Bora para o último?
Passo 7
Para os valores de e são:
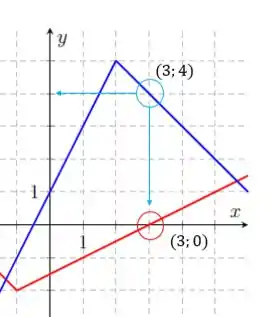
Os valores são
E agora as derivadas. Primeiro de em vermelho
A derivada é a mesma do passo anterior, já que a cara da função não mudou. então
Assim
Passo 8
Os quatro valores:
Agora é aplicar na regra:
Ufa! Terminamos!
Espero ter ajudado!
Até a próxima!