4. Resolva as seguintes questões.
- Mostre que a afirmação “qualquer função possui no máximo uma assíntota horizontal” é falsa, usando a função .
- Dada , , use a definição de derivada para mostrar que .
- Uma demonstração errada do item acima é a seguinte:
Seja , onde e , pela regra do produto, e como tem-se .
Encontre o erro na demonstração acima.
Passo 1
- Oi, galerinha! Tudo bom? Aqui temos três perguntinhas para responder, onde em cada uma vamos usar um conhecimento diferente!
- Para mostrar que , vamos ter que dividir a nossa função em duas partes, pois temos um módulo ali.
- O erro desta demonstração é que a nossa função possui uma mudança de comportamento em . Ou seja, a função não tem derivada naqueel ponto, por isso não podemos aplicar a regra do produto.
Começando pela letra a, temos que mostrar que a nossa tem duas assíntotas horizontais, para confirmar que aquela afirmação entre aspas é falsa.
Para quem não lembra, para encontrarmos assíntotas horizontais, temos que fazer o limite da nossa função tendendo a . Ou seja,
Bora lá!
Passo 2
Começando por,
Repara que caímos em uma indeterminação, para sair dela, vamos colocar o nosso em evidência
Ou seja, temos uma assíntota horizontal em
Agora vamos fazer
Ou seja, temos outra assíntota horizontal em . Logo, a afirmação é falsa!
Passo 3
Para , temos que a nossa função será
Com isso temos que,
Já para , temos que nossa função será
E a derivada ficará,
Beleza?
Passo 4
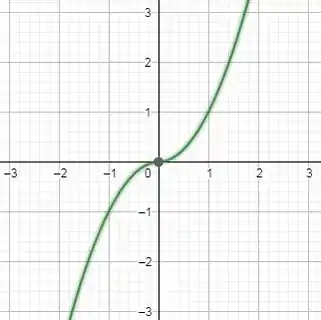
Inclusive, pessoal, esse foi o motivo pelo qual dividimos a função em duas partes na demonstração da letra b.
Resposta
No texto.