Questão 1.1: Seja uma função contínua tal que , , , e . Considere as seguintes afirmações:
(a) A reta se intersepta com o gráfico de exatamente vezes.
(b) A reta se intersepta com o gráfico de pelo menos vezes.
(c) A reta se intersepta apenas uma vez com o gráfico de .
(d) A reta não se intersepta com o gráfico de .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão foi dada algumas imagens de uma função entre e . é uma função contínua e , , , e são as imagens que foram dadas para a gente.
Com essas informações, temos que analisar algumas alternativas e assinalar qual é a alternativa que melhor se encaixa na nossa situação.
Entendeu? Como podemos fazer isso? 🤔
Como foi dito que é contínua, vamos plotar os pontos das imagens dadas no plano cartesiano e ligá-los da maneira mais simples, assim, “esboçamos” o gráfico de , que vai nos ajudar.
Vamos analisar alternativa por alternativa...
Pronto? 😎
Passo 2
Plotando os pontos e ligando os pontos através de seguimentos de retas, vamos obter algo que poderia ser nossa função .
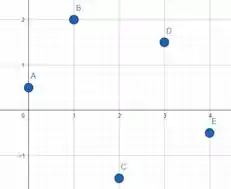
No item a) foi dito que a reta intercepta exatamente vezes.
Será mesmo? 🤔
Esboçando a reta , temos
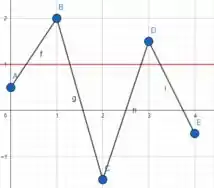
Podemos ver que realmente intercepta vezes, porém apenas a partir dos pontos que nos deram. Por exemplo, se em a função for e em a função for ...
Essa é uma possibilidade que faria a reta cortar o gráfico de mais de vezes e não podemos afirmar que isso não acontece.
Logo, essa afirmação é falsa.
Entendeu? Bora pra outra! 😉
Passo 3
Na alternativa b) diz que a reta intercepta pelo menos vezes.
O que acha? 👀
Como acabamos de discutir no passo anterior. Não sabemos o comportamento da função nos intervalos entre os pontos dados, portanto, pode ser que a reta intercepte mais que vezes.
Sendo que dizer que a reta intercepta pelo menos vezes está correto.
Logo, a alternativa b) é a correta!

Vamos continuar analisando as outras alternativas para ver o porquê são falsas.
Partiu? 😁
Passo 4
Na alternativa c) diz que a reta intercepta apenas uma vez.
Suspeito, não é? 👀
Perceba que a função começa em com uma imagem de e termina em com uma imagem de .
Ou seja, se assumir valor em algum momento, ela tem que subir e descer assim, interceptando a reta duas vezes.
Ou também pode ser que a função não adquira imagens maior que , fazendo com que a reta não intercepte nenhuma vez.
Como não temos a definição exata de , podemos dizer que a alternativa c) é falsa.

Bacana, não é? 😎
Passo 5
E por fim, a alternativa d) diz que a reta não se intersepta com o gráfico de .
E aí? 🤔
Com base nas afirmações anteriores das alternativas, podemos dizer que essa é falsa pois é possível que possua imagens menores que nos intervalos entre os pontos dados, mas que não conseguimos ver.
Então, a alternativa d) é falsa!
Portanto, a alternativa que melhor se encaixa na nossa situação, é a alternativa b)!
É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta
(b) A reta se intersepta com o gráfico de pelo menos vezes.