Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema do Valor Intermediário

Ver Teoria
Exercício 35123456789101112131415161718192021222324252627282930313233343637383940414243444546474849505152535455565758596061626364656667686970717273747576

Enunciado

Q05) Use o teorema do valor intermediário (TVI) para mostrar que a equação

sin ⁡ x = 4 - 2 x

Tem uma solução no intervalo 0 , π 2 . Relembre que π ≅ 3,14

Passo 1

Já que a questão já da a dica pra gente que é pra usar o TVI, vamos dar uma lembrada nela. Seja f uma função contínua que passa pelos dois pontos azuis abaixo:

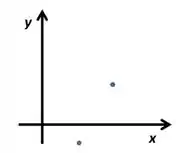
Pelo TVI, é impossível ligar os dois pontos sem passar o eixo x . Ou seja, o TVI prova que existe pelo menos uma raiz pra essa função contínua. Mas como que isso se aplica aqui. Veja bem:

sin ⁡ x = 4 - 2 x

A função sin ⁡ x é contínua, certo? Assim como o polinômio 4 - 2 x . E se eu estabelecesse uma função tal que:

sin ⁡ x = 4 - 2 x

sin ⁡ x - 4 + 2 x = 0

f x = 0

Opa, gerei uma função f x = sin ⁡ x - 4 + 2 x e disse que ela é igual a 0 então! Pra responder a questão basta então provar que essa minha função contínua gerada tem pelo menos uma raiz no intervalo 0 , π 2 . Pra provar isso, uma boa primeira estratégia é substituir x pelos valores extremos do intervalo:

f 0 = sin ⁡ 0 - 4 + 2 ∙ 0 = 0 - 4 + 0 = - 4 < 0

f π 2 = sin ⁡ π 2 - 4 + 2 ∙ π 2 = 1 - 4 + π ≅ 0,14 > 0

E olha só! Um deu negativo e outro positivo! Ta provado então. De uma forma mais bonitinha, podemos dizer:

Seja f x = sin ⁡ x - 4 + 2 x uma função contínua, com f 0 < 0 e f π 2 > 0 , então existe pelo menos um c ∈ 0 , π 2 tal que f c = 0 e logo sin ⁡ c = 4 - 2 c

Resposta

Seja f x = sin ⁡ x - 4 + 2 x uma função contínua, com f 0 < 0 e f π 2 > 0 , então existe pelo menos um c ∈ 0 , π 2 tal que f c = 0 e logo sin ⁡ c = 4 - 2 c

Exercícios de Livros Relacionados

Use o Teorema do Valor Intermediário para mostrar que existe uma raiz da equação dada no intervalo especificado f x = x 3 = 1 - x ,( 0 ,1 )
( a ) Demonstre que a equação tem pelo menos uma raiz real. ( b ) Use sua ferramenta gráfica para encontrar a raiz correta até a terceira casa decimal. f x = a r c t gx + 1 - x
Use o Teorema do Valor Intermediário para mostrar que existe uma raiz da equação dada no intervalo especificado ln ⁡ x = e - x , ( 1,2 )
Se f x = x 2 + 10 s e n x , mostre que existe um número c tal que f c = 1000
Seja f : a , b → R uma função contínua e suponha que f não seja constante em a , b . Prove que existem números reais m e M , com mM , tais que Im ⁡ f = m , M .(Observação: Imagem de f = Im ⁡ f = f x |