A partir dos gráficos abaixo, justifique, se para cada função:

1. A tese do Teorema do Valor Intermediário é satisfeita.
2. A hipótese Teorema do Valor Intermediário é satisfeita.

Obs: A tese pode ser interpretada como o “resultado” de um teorema. A hipótese pode ser interpretada como a “condição” para que o teorema funcione.

a):

b):

c):

Vamos lá:

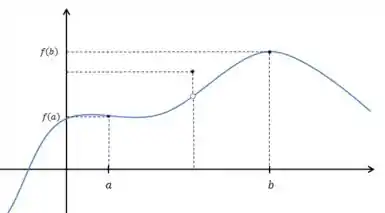
a):

Primeiro:

A função é contínua em ? Não, tem uma descontinuidade ali no gráfico.

Porém, se você reparar bem, para todos os pontos da função naquele intervalo, sempre existe um que gera o valor da função nesse ponto, e sempre pertence a .

Isso acontece mesmo na descontinuidade com um salto!!!!.

Então, mesmo a função sendo descontínua:

A tese é atendida.

A hipótese não é atendida.

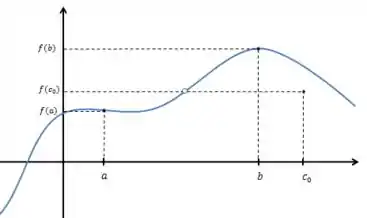
b):

Vamos lá de novo:

Primeiro:

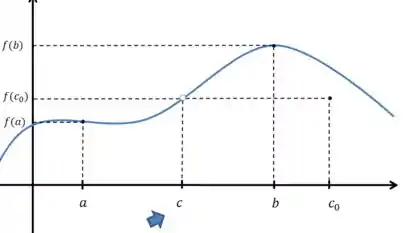
A função é contínua em ? Não, Ela também possui uma descontinuidade. Porém, vamos analisar essa descontinuidade:

Ela acontece no correspondente ao Mas onde está esse Dentro do intervalo

Não, ele não tá ali, pois . Isso quebra o resultado do teorema, pois dentro do intervalo vai existir um número cuja imagem na função não existe. Ou seja, não existe para o da imagem abaixo:

Então:

A tese não é atendida.

A hipótese não é atendida.

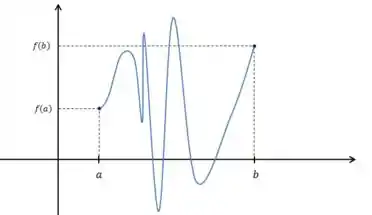
c):

Vamos lá de novo:

Primeiro:

A função é contínua em ? Sim! Claramente contínua.

A pergunta é: Existe o tal do Claro que sim! Se a tese e a hipótese são atendidas, o teorema tem o seu sentido completo!

Na verdade, existem vários , se você procurar, como por exemplo:

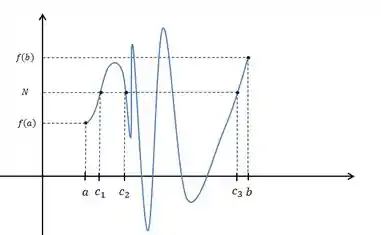
Então:

A tese é atendida.

A hipótese é atendida.