29) Dê um exemplo de uma função tal que em dois pontos distintos e tem sinais contrários, não é contínua no intervalo e a tese do Teorema do Valor Intermediário é falsa.
Passo 1
Eaí pessoal, tudo certinho com vocês?
Bom, essa questão pede pra gente dar um exemplo de uma função que tenha uma descontinuidade em um intervalo , que e tenham sinais contrários, mas que não obedeça ao T.V.T(teorema do valor intermediário).
Bora começar revisando esse teorema, que diz o seguinte:
“Se uma função contínua troca de sinal num certo intervalo, então ela tem ao menos uma raiz nesse intervalo.”
Beleza, precisamos pensar qual função é um bom exemplo.
Passo 2
A ideia aqui é que uma forma da função não obedecer ao T.V.T é ela não ter raiz real, e a sua descontinuidade é o motivo que faz ela trocar de sinal em pontos e . Existem algumas funções clássicas que não possuem raiz real, justamente por causa da sua descontinuidade.
A mais conhecida é a hipérbole, que tem equação .
Esse exemplo é bem interessante porque a descontinuidade ocorre exatamente em . Vamos ver como fica o seu gráfico:
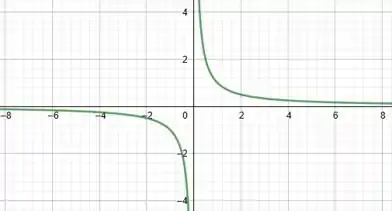
Portanto, se a gente escolher, por exemplo, o intervalo , teremos uma função descontínua, em que e , e que não obedece ao T.V.T.
Prontinho, é ela mesmo que será a nossa resposta 😊
Resposta
em .