30) Se uma função muda de sinal quando varia de um ponto para o ponto , existirá obrigatoriamente um ponto entre e onde a função se anula? Justifique sua resposta.
Passo 1
Faaaala galeraaa! Todo mundo animado pra matar mais uma questão?
Esse exercício nos faz uma pergunta bem interessante. Ele quer saber se sempre que uma função muda de sinal de um ponto para outro, ela necessariamente precisa passar pelo zero, ou seja, se anula.
Para começar, precisamos identificar de que teorema ela está fazendo referência. É o T.V.T (Teorema do Valor Intermediário), que diz o seguinte:
“Se uma função contínua troca de sinal num certo intervalo, então ela tem ao menos uma raiz nesse intervalo.”
A chave aqui está na palavra contínua. Vamos ver isso melhor!
Passo 2
Se uma função for continua em um dado intervalo, realmente não é possível termos dois pontos onde ela troca de sinal, sem termos raiz em .
Um jeito simples de pensar nisso é imaginar que estamos desenhando o gráfico de num papel. Se começamos a desenhar em um ponto abaixo do eixo x, não é possível passarmos para a parte de cima sem cruzarmos o eixo das abcissas.
Então o nosso exemplo vai ser simplesmente uma função que seja descontínua, e que essa descontinuidade seja o motivo dos sinais diferentes em e .
Um ótimo exemplo é a hipérbole . Vejamos o seu gráfico:
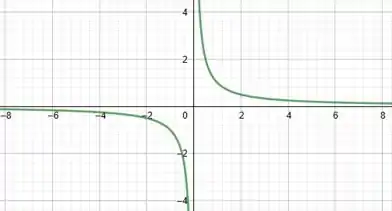
Podemos notar que:
Então nossa resposta à questão é Não! Existem funções que obedecem às condições do enunciado, mas que não são contínuas e não se anulam em nenhum ponto.
Resposta
Não! é um contraexemplo.