Um monge tibetano deixa o monastério às 7 horas da manha e segue sua caminhada
usual ate o topo da montanha, chegando lá as 7 horas da noite. Na manhã seguinte ele parte
do topo as 7 horas da manha e, andando pelo mesmo caminho, chega no monastério as 7
horas da noite. Mostre que existe um ponto no caminho que o monge vai cruzar exatamente
na mesma hora do dia em ambas caminhadas.
Passo 1
O primeiro passo vai ser a gente estudar o movimento de ida e volta pro topo da montanha pra entendermos o que está acontecendo. Saca só:
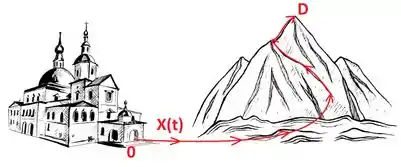
Vamos chamar então como a posição na ida em função do tempo e estabelecer como posição o monastério e como posição o topo da montanha. Se o monge saiu as da manhã e chegou as da noite, temos:
Agora, pra volta, temos:
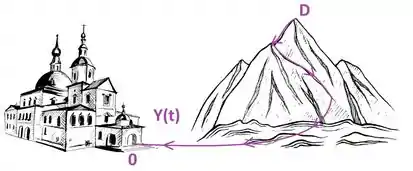
A ideia aqui é a mesma. vai ser a posição na volta em função do tempo. Se as da manhã do dia seguinte ele parte do topo da montanha e chega as da noite no monastéria, temos:
Passo 2
Agora que modelamos matematicamente a ideia, vamos pensar aqui: que tipo de função é e ? Pensa aqui comigo: será que é possível existir algum valor de , tempo, na qual a posição, seja na ida ou na volta, não esteja definida? Não né? Não importa qual tempo a gente escolha ele vai sempre estar em algum lugar do trajeto! Em outras palavras, tanto quanto vão ser contínuas!
Beleza, mas e daí? Veja só. Se vai existir um ponto do trajeto que ele vai passar tanto na ida quanto na volta na mesma hora, isso quer dizer que:
Ou seja, a posição na ida em uma hora qualquer do dia vai ser a mesma posição na volta na mesma hora do dia.
Agora veja, se e são funções contínuas, então a função:
Também vai ser, e vamos ter que
E olha só olha lá: vai ser um zero da função ! Podemos extrair outras informações sobre levando em consideração o trajeto. Saca só:
E é ai que ta o pulo do gato! Se:
Então, pelo Teorema do Valor Intermediário, existe um tal que . Se esse de fato existe, então de fato:
E nosso querido monge acaba passando na mesma hora do dia no mesmo ponto sim!