Seja uma função contínua em ℝ tal que e , e seja . A função composta possui duas raízes negativas distintas. Determine intervalos abertos disjuntos contendo cada uma dessas raízes.
Passo 1
Bom, a questão pede os intervalos contendo as raízes, isso nos dá um indício de que vamos usar o teorema do valor intermediário (TVI).
Só relembrando, o TVI serve para provar que a função passa por qualquer ponto , desde que exista pontos menores que e maiores que e a função seja contínua no intervalo formado por eles.
Como estamos buscando raízes, o ponto que estamos falando é
Então agora vamos procurar pontos menores e maiores que ele, ok?!
Passo 2
Então, galerinha, o problema nos forneceu duas informações importantes. A primeira é,
ou seja, é dependente de .
Tá mas o que a gente faz com isso? Aí que entra segunda informação importante:
Ainda não se ligou? Vamos olhar estes pontos no gráfico cartesiano são assim:
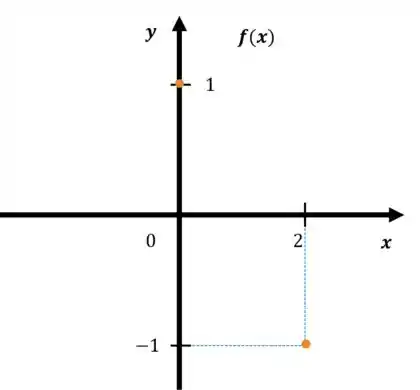
Lembra que ele disse que é continua? Então, repara que para ligar os pontos amarelos eu preciso passar pelo . Ou seja, a gente pode aplicar o TVI neste caso.
Mas o que falta agora? Lembra que,
Então vamos ter que achar valores de que sejam igual a e , pois são os pontos em que nós conhecemos.
Isso significa que a função troca de sinal entre e .
Passo 3
Igualando, podemos descobrir quais valores de fazem ser igual a 0 e 2:
Resolvendo a equação de segundo grau, as soluções de estão no conjunto abaixo:
Ou seja, quando eu tiver igual a e , o nosso será .
No plano cartesiano vamos ter os seguintes pontos de
Isso porque fizemos
Analogamente, as soluções de estão no conjunto abaixo:
Isso resulta nos seguintes pontos de
Isso porque fizemos
No gráfico cartesiano de , teríamos o seguinte:
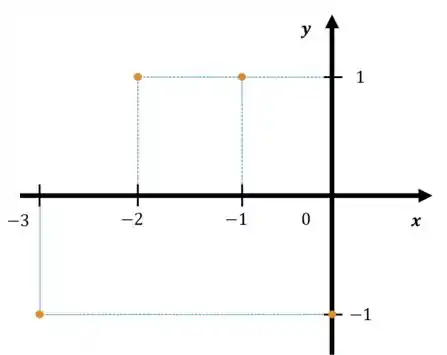
Passo 4
Portanto, como podemos ver, a função troca de sinal no intervalo:
E também no intervalo:
E pelo teorema do Valor Intermediário, temos que existe ao menos uma raiz em cada um desses intervalos, conforme queríamos demonstrar.