Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Máximos e Mínimos

Ver Teoria
Exercício 326123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPE – Cálculo 1 – Listas Prof. Jose Carlos de Albuquerque – Questão 4a

Analise

  1. Os intervalos nos quais f é crescente ou decrescente;
  2. Os valores máximo e mínimo locais de f ;
  3. Os intervalos de concavidade e os pontos de inflexão;

a )   f x = 2 x 3 + 3 x 2 - 36 x

Passo 1

Oi, tudo bem?

O problema nos deu essa função aqui

f x = 2 x 3 + 3 x 2 - 36 x

E pediu para calcularmos intervalos de crescimento/decrescimento, valores de máx/mín, intervalos de concavidade e pontos de inflexão. Vamos relembrar como se acha cada uma dessas coisas?

  • Intervalos de crescimento/decrescimento: intervalos onde a derivada é positiva/negativa. Então a ideia aqui é achar a derivada e fazer o estudo do sinal dela;
  • Máx/mín locais: são pontos onde a derivada troca de sinal (mais pra menos = máximo; menos pra mais = mínimo);
  • Intervalos de concavidade e inflexão: é o estudo da segunda derivada. Concavidade positiva/negativa = segunda derivada positiva/negativa. E os pontos de inflexão é onde ela é zero. Então a ideia aqui é derivar de novo, igualar a zero e estudar o sinal da função

    • Beleza?

    Bora começar?

    Vou fazer passo a passo com você!

    Passo 2

    Agora vamos começar derivando a função

    f x = 2 x 3 + 3 x 2 - 36 x

    f ' x = 6 x 2 + 6 x - 36

    Igualando a zero achamos dois pontos

    6 x 2 + 6 x - 36 = 0

    x = - 3   e   2

    Agora vamos fazer o estudo do sinal da derivada em torno desses pontos

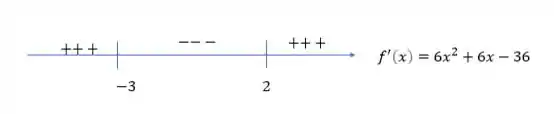
    Tudo bem até aqui? Agora vamos as conclusões:

  • Crescimento: - ∞ ; - 3 U 2 ; + ∞
  • Decrescimento: - 3 ; 2
  • Ponto de máximo local: x = - 3
  • Ponto de mínimo local: x = 2

    • Beleza?

    Passo 3

    Agora vamos para o estudo da segunda derivada:

    f ' x = 6 x 2 + 6 x - 36

    f ' ' x = 12 x + 6

    12 x = - 6 → x = - 1 2

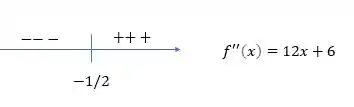    E o sinal em torno desse ponto

    Nossas conclusões:

  • Concavidade positiva: - 1 2 , + ∞
  • Concavidade negativa: - ∞ ; - 1 2
  • Ponto de inflexão: x = - 1 2

    • Beleza? Espero ter ajudado!

    Resposta

  • Crescimento: - ∞ ; - 3 U 2 ; + ∞
  • Decrescimento: - 3 ; 2
  • Ponto de máximo local: x = - 3
  • Ponto de mínimo local: x = 2
  • Concavidade positiva: - 1 2 , + ∞
  • Concavidade negativa: - ∞ ; - 1 2
  • Ponto de inflexão: x = - 1 2

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 ⁡ x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)