Um barco deixa as docas às 14h e viaja para o sul com velocidade de 20km/h. Outro barco

estava rumando para o leste a 15km/h e alcança a mesma doca às 15h. Em que momento os

dois botes estavam mais próximos um do outro?

Eaew, belezinha?

A questão nos descreve nos descreve uma situação em que um barco se aproxima e o outro se afasta das docas. Como o barco vindo do leste com velocidade 15km/h atinge as docas às 15h, isso significa que, às 14h, esse barco se encontrava à 15km à oeste das docas. A figura abaixo ilustra a situação, com o barco em verde se aproximando das docas pelo oeste e o barco vermelho se afasta para o sul.

Com isso, considerando a doca como origem, podemos escrever que, a partir das 14h, a função que determina a trajetória do barco verde é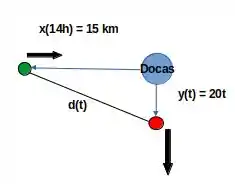

Às 14h, o barco em vermelho se afasta para o sul, com velocidade de 20km/h. Assim, podemos escrever uma função para a sua trajetória

Assim, podemos também encontrar uma função para a distância d(t) entre os barcos através do teorema de Pitágoras

Então, para descobrir em que momento a distância entre os barcos é a menor, precisamos encontrar o ponto de extremo dessa função. E como a gente faz isso? Bem, a gente sabe que em um ponto de extremo, a derivada de uma função é nula! Então, a gente precisa derivar a função distância para determinar em que instante de tempo ela ocorre! Então vamos lá derivar!