UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 29iie
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
A função assume máximo ou mínimo absoluto? Em caso afirmativo, quais são estes
valores?
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de cálculo . Nosso objetivo é verificar se assume máximo ou mínimo absoluto.
Como encontramos esses máximos e mínimos? É o famoso deriva e iguala a zero. Mas para garantirmos que os pontos serão de máximo ou de mínimo, precisamos olhar o sinal da segunda derivada.
Se o sinal da segunda derivada for positivo, então é ponto de mínimo e se for negativo, é ponto de máximo.
Na letra já calculamos a derivada
e vimos que ela vale zero quando
Passo 2
Agora, vamos calcular a segunda derivada e verificar seu sinal.
Usando a regra da cadeia e a regra do produto, temos que:
Agora, quando que essa segunda derivada é zero? Ora, quando
que é uma equação do segundo grau. Cujas raízes são:
Logo temos que Logo esses são os pontos onde a nossa segunda derivada é zero. Vamos verificar o sinal da nossa derivada para os valores onde , , ,
Começando com .
Se , então
Se, então
se , então
Na reta real ficaria assim.
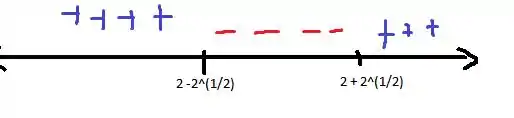
Passo 3
Agora que sabemos os sinais da segunda derivada e os pontos onde a primeira derivada é zero, podemos verificar os pontos de máximo ou mínimo globais
A primeira derivada é nula em
Como o sinal da segunda derivada em é positiva, então esse será um ponto de mínimo local. Mas é de mínimo global? A resposta é sim. Pois como vimos
E quando , o sinal da segunda derivada é negativo. Logo esse é um ponto de máximo local, mas não será de máximo global. Uma vez que
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima