Considere a função
Determine suas assíntotas (caso existam), intervalos de crescimento e decrescimento, pontos críticos, máximos e mínimos locais (caso existam), analise a concavidade e encontre pontos de inflexão (caso existam) e, por fim, esboce o gráfico da função, destacando os elementos anteriores.
Passo 1
Determinar as assíntotas
Essa questão pediu tanta coisa que só faltou pedir pra fazer um cafezinho também. Mas bem, questão é questão então vamos lá. Primeiro, pra determinar as assíntotas, temos que ver se a função não tende a nenhum valor quando:
Para achar as assíntotas horizontais, tudo que a gente tem que fazer é calcular o limite. Pra começar, da uma olhada:
Quando fica infinitamente grande e positivo, todo fica infinitamente grande também. Ou seja, sem assíntotas aqui. Agora, quando fazemos:
Com infinitamente grande, porém negativo, vai virar um número infinitamente pequeno, pois se reescrevermos o sinal de negativo, seria o mesmo que para infinitamente grande e positivo. O limite disso é . Sendo assim:
Opa, então a reta é uma assíntota horizontal dessa . Pra ver as assíntotas verticais, basta a gente checar algum valor de que “dê ruim” na função. Em matematiquês, que resulte em alguma descontinuidade. Como aceita qualquer , então não vamos ter assíntotas verticais.
Passo 2
Encontrar a primeira derivada
Esse tipo de questão sempre vai pedir da gente o teste da primeira derivada, beleza? Guarda na cachola isso porque pra acharmos tudo que a questão pede, temos que saber o comportamento da reta tangente a curva ao longo da curva. E como a primeira derivada nos da a inclinação da reta tangente, partiu derivar:
Passo 3
Achar os pontos críticos
Pontos críticos são todos os pontos em que a primeira derivada é nula. Sendo assim, temos que fazer:
Logo de cara, conseguimos ver que é uma solução. E como é um número sempre positivo e nunca nulo, vai ser a única solução, tudo bem? Então show de bola, encontramos a raíz da primeira derivada. Usando esses valores de na função original, vamos ter:
O único ponto crítico vai ser então:
Passo 4
Classificar o ponto crítico
Pra gente saber se um ponto crítico é de mínimo, máximo ou de inflexão, temos que lembrar que:

E se nenhum dos dois aplicar, ai no caso temos um ponto de inflexão, beleza? Então vamos assumir que por exemplo e checar os pontos:
Portanto, vamos ter que:
Passo 5
Achar os intervalos de crescimento e decrescimento
Crescimento e decrescimento tem tudo a ver também com a inclinação da reta tangente! Afinal, desde a invenção da máquina de lavar, quando a inclinação é negativa, a função é decrescente e quando é positiva, a função é crescente. Então vamos olhar bem para:
Com a raíz
Vamos ver então o que acontece em intervalos que envolvam a raíz. Isto é:
No primeiro intervalo, vamos pegar qualquer . Por exemplo,
No quarto intervalo, vamos pegar qualquer .Porexemplo,
Analisando os resultados e seus sinais, a gente chega a conclusão que:
Passo 6
Analisar a concavidade
Pra analisar a concavidade vamos ter que fazer o teste da segunda derivada. Pra refrescar a memória:

Maravilha, vamos então achar a segunda derivada
Agora se , vamos ter:
Agora se , vamos ter:
Por fim:
Passo 7
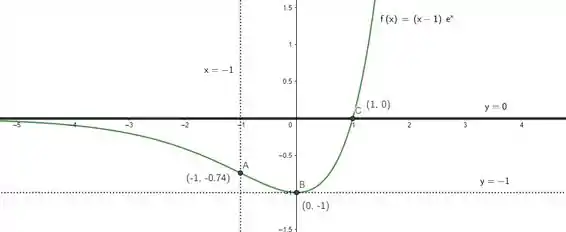
Esboçar o gráfico
É, pra esboçar o gráfico na mão vai dar um trabalhinho porque vamos ter que destacar tudo que vimos anteriormente. Mas, no final das contas, vai ficar assim:
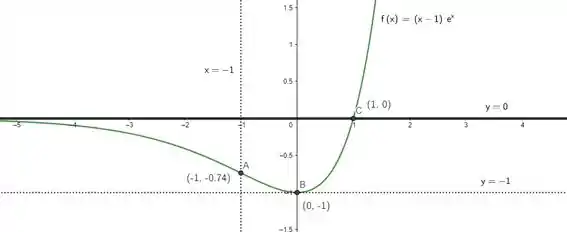
Resposta