Considere a função e determine

1. O domínio de
2. Os intervalos onde é estritamente crescente e decrescente
3. Os intervalos de convexidade (concavidade pra cima) e concavidade (concavidade pra baixo)
4. Os pontos de máximo e mínimo (se houver)
5. As assíntotas verticais e horizontais (se houver)

b) Intervalos de crescimento e decrescimento

Próxima letra então. Quando falamos de crescimento e decrescimento temos que olhar pra inclinação da reta tangente, beleza? Se negativa, decresce. Se positiva, cresce. E como a inclinação da reta tangente é a primeira derivada, partiu derivar:

Vamos ver agora quando a função muda de sinal, ok? Pra isso, primeiro a gente iguala a . Saca só:

Elevando os dois lados ao quadrado:

Beleza, daí já dá pra ver que é uma solução. Divindo por dos dois lados para achar as outras, temos:

E logo:

Ok, achamos três valores, mas vamos dar uma olhada direitinho neles, porque como a primeira derivada tem essa cara:

Nenhum valor negativo ou igual à podem entrar ai! Opa, sobra então só:

Nesse caso, vamos ver o que acontece com o sinal da derivada pra valores maiores e menores que . Pra valores menores, por exemplo , temos:

E pra valores maiores, como por exemplo, temos:

Fechamos essa letra então. A função vai ser então

c) Análisar os intervalos das concavidades

Pra gente analisar as concavidades vamos precisar agora da segunda derivada. Isso mesmo, vamos ter que derivar de novo. Mas relaxa, vamos com calma que chegamos lá. A segunda derivada então vai ser:

Pra analisar o sinal, vamos ver em que ponto que o sinal muda, beleza? Igualando à , temos:

Elevando ao quadrado os dois lados:

De novo, já vemos que é uma solução. Então partindo pras próximas, dividindo os dois lados por , ficamos com:

Aqui a ideia é a mesma da letra anterior: valor negativo e nulo não rola. Então vamos considerar só o valor dos três que achamos. Testando valores menores primeiro, como por exemplo, temos:

E pra valores maiores, como por exemplo, temos:

A concavidade então vai ficar pra cima quando a segunda derivada for positiva e pra baixo quando for negativa.

d) Pontos de máximo e mínimo

Pra gente saber pontos de máximo e mínimo, precisamos de informações da primeira derivada, beleza? Afinal, esses pontos são pontos críticos! Como vimos na letra (b), o único ponto crítico é . Opa, agora é só rever os sinais da derivada antes e depois desse ponto:

Se antes a inclinação era negativa e depois virou positiva, esse único ponto crítico é então um ponto de mínimo. Pra achar a coordenada então, fazemos:

O ponto de mínimo vai ser então:

e) Assíntotas verticais e horizontais

Pra ver assíntotas a gente vai ter que usar limites e ver como a função se comporta neles, beleza? Vamos começar com as verticais. Pra falar delas, vamos lembrar do domínio da função:

Com esse domínio aí, qualquer valor maior que não dá problema na função. Mas o que será que acontece no próprio ? Só o limite sabe. Então vamos perguntar pra ele:

O primeiro limite, vai dar:

Já o segundo limite, quanto mais próximo de , menor o denominador como um todo. O número 1 dividido por um número infinitamente pequeno e positivo vai dar então:

Enfim, temos que:

Então é sim uma assíntota vertical! Maravilha, falta pra fechar a questão a assíntota horizontal. De novo a gente usa os limites, beleza? Mas agora, com o . Partiu calcular então:

O primeiro limite da porque a raiz de um número infinitamente grande continua um número infinitamente grande. Agora, se a gente dividir o número um por um número grande desses, resta quase nada, ou seja, resta próximo de . Sendo assim:

E por fim:

Ou seja, a função não tem assíntotas horizontais.

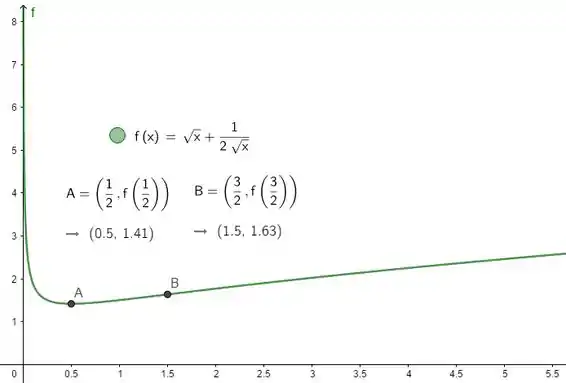
Adimirar o gráfico da função

Pra gente ver que fez tudo certo, dá uma olhada no gráfico dessa função: