UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 9.2
Dada a função , obtenha seus pontos de máximo e mínimo relativos e absolutos, sabendo-se que o domínio é D = [0; 6].
Passo 1
Eaew, belezinha?
O enunciado da questão pede para a gente encontrar os máximos e mínimos absolutos da função , no intervalo . E como é que a gente faz isso? Bem, em um ponto de máximo, a função não cresce a partir desse ponto, caso contrário ele não seria um máximo. E, em um ponto de mínimo, a função não diminui a partir desse outro ponto, se não ele não seria um ponto de mínimo. Assim, a gente pode utilizar essa informação para descobrir esses pontos! Imagina a seguinte situação: conforme você vai aumentando o valor de x, a função vai crescendo e crescendo até atingir seu valor máximo. A partir daí, ela tem que decrescer (para que esse ponto tenha sido máximo). Bem, a gente sabe que a derivada de uma função nos dá a taxa de variação dela em relação à variável do domínio. Então, para calcular os pontos de extremos, só precisamos exigir que a derivada seja nula, porque, para ser um ponto de extremo (ou de inflexão) de uma função contínua, a derivada tem que mudar de sinal! Se nos aproximamos de um ponto de máximo, a derivada deve ser positiva pois a função está crescendo para atingir seu máximo. Agora, após passar esse ponto, a derivada tem que ser negativa, porque a função tem que decrescer a partir do máximo, ou então ele não seria um máximo da função. O mesmo raciocínio vale para pontos de mínimo: a derivada deve ser negativa até atingir o ponto de mínimo e, a partir daí, positiva.
Outro ponto importante a se notar é que, uma função quadrática com concavidade negativa possui um máximo absoluto mas não possui mínimo: conforme x vai à mais ou menos infinito, a função decresce infinitamente. Mas aqui a gente tá lidando com um intervalo finito, então a função vai “truncada” e possuir algum valor mínimo nesse intervalo. Sacou? Então vamos lá calcular a função nos limites do intervalo e a derivada!
Passo 2
Como a derivada de uma soma de funções é simplesmente a derivada da soma, só precisamos derivar cada um dos termos de y(x). A gente sabe que a derivada de x é 1 e a derivada de é 2x . Então, a derivada da nossa função é
Agora, a gente só precisa descobrir qual ponto no intervalo anula essa função! Assim, temos
Então, o valor de x que maximiza essa função é 5, onde ela assume o valor . Agora, só precisamos descobrir quais são os valores da função f(x) nos limites do intervalo para descobrir qual é o valor mínimo da função em [0,6]. Bora lá!
Passo 3
Substituindo os dois limites do intervalo [0,6] na função, obtemos
e
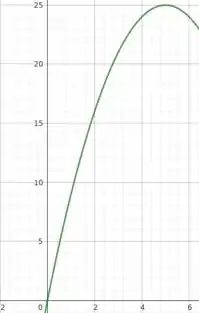
Então, a gente vê que, nesse intervalo, o menor valor que a função assume é em x=5, quando a função é nula e, o maior valor que a função assume é em x=5, quando a derivada é nula e a função quadrática atinge seu máximo absoluto. A partir de x=5, a função começa a decrescer, até atingir o valor 24 em x=6, que não representa nem um máximo nem um mínimo da função nesse intervalo. Dá só uma olhada no gráfico da função no intervalo [0,6]:
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ponto de máximo absoluto:
Ponto de mínimo no intervalo [0,6]: (0,0)