UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 1e.
- Defina:
- Máximo relativo e máximo absoluto de uma função.
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão pede para definir o que é o máximo relativo e o máximo absoluto de uma função. Correto?
E o que podemos perceber pela é que existe uma diferença entre eles. Já que o problema pede para que a gente defina os dois.
Então vamos começar por partes aqui. Vamos primeiro entender o que significa o máximo de uma função, e depois a gente diferencia o máximo relativo do máximo absoluto. Beleza?!
Vem comigo que te ajudo com isso.
Passo 2
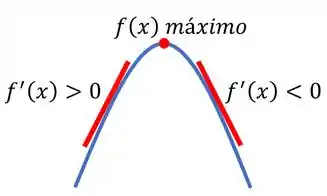
Um ponto de máximo é um ponto na função que é maior que os pontos próximos a ele. Em um gráfico, é como se tivéssemos o topo de uma colina:
Se a gente olhar com calma, vamos perceber nesses pontos de máximo a reta tangente à função é horizontal, ou seja, o coeficiente angular dela é zero.
E você se lembra que o coeficiente angular da reta tangente à um ponto é justamente a derivada da curva naquele ponto? Então, a gente acabou de chegar à conclusão de que para pontos de máximo a derivada da curva é nula naquele ponto, ou seja, se em temos um ponto que pode ser de máximo:
Mas cuidado, porque os pontos de máximo não são os únicos em que a derivada da função vai a zero. Isso também pode acontecer em pontos de mínimo ou pontos de sela.
Então devemos fazer teste para saber se o pondo encontrado ao fazer a derivada igual a zero é mesmo um ponto de máximo.
Passo 3
Para saber se o ponto é mesmo um ponto de máximo, podemos fazer o teste da primeira derivada. Que consiste em analisar o sinal das derivadas da função em pontos próximos ao que estamos analisando. Assim, se a derivada em um ponto anterior ao nosso ponto for positiva e a derivada em um ponto posterior for negativa, estamos trabalhando com um ponto de máximo.
Show, mas agora vamos diferenciar o ponto de máximo local e máximo global. Beleza?
Passo 4
Nem sempre que achamos um máximo da função, esse vai ser exatamente o maior valor que a função pode assumir. Olha só essa função aqui:
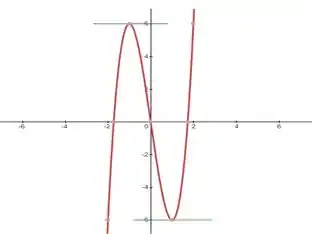
Vemos que para temos um máximo, mas se olharmos pelo gráfico conseguimos ver que a função pode atingir valores maiores, é só pegar um um pouco maior e vamos perceber que o ponto de máximo não reflete o maior valor que a função pode assumir, né?
Nesses casos, falamos que o ponto que nós achamos, é na verdade ponto de máximo local. Caso de fato ele seja o maior valor que a função assuma, nós o chamaremos de máximo global ou absoluto.
Para determinar se esses caras são globais ou locais, devemos sempre ficar de olho nos extremos da nossa função. Olha aqui esse exemplo de uma função definida no intervalo ]:
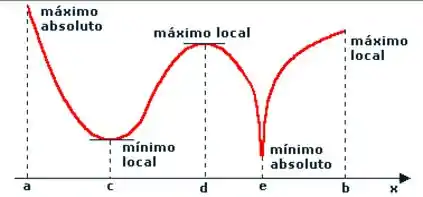
Repare que, se quiséssemos achar um ponto de máximo, derivando a função e realizando os testes das derivadas, iríamos achar o ponto , sendo um máximo.
Porém, o ponto NÃO é o ponto de máximo global, mas sim o ponto , no extremo do intervalo analisado. Por isso, é importante testar e (extremos do intervalo) e compará-los com no ponto crítico anteriormente encontrado.
E assim respondemos mais uma questão. Bora olhar a próxima!
Resposta
No desenvolvimento.