1. Defina:

1. Número crítico.

Pontos críticos de uma função são pontos em que algo de importante está acontecendo com ela.

Esses pontos podem ser pontos de máximo, pontos de mínimo ou ponto de sela da função.

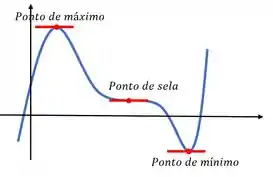
Eles são obtidos pela reta tangente ao gráfico da função. E você se lembra que o coeficiente angular da reta tangente à um ponto é justamente a derivada da curva naquele ponto? Então, a gente acabou de chegar à conclusão de que para pontos críticos a derivada da curva é nula naquele ponto, ou seja, se em temos um ponto crítico:

E para saber qual a classificação do ponto e descobrir se ele é um ponto de máximo, de mínimo ou ponto de sela, podemos fazer o teste da primeira derivas.

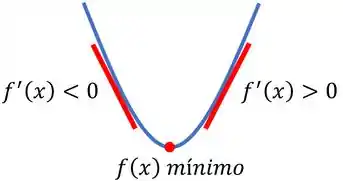
Para saber se o ponto é um ponto de mínimo, fazemos o teste da primeira derivada. Que consiste em analisar o sinal das derivadas da função em pontos próximos ao que estamos analisando. Assim, se a derivada em um ponto anterior ao nosso ponto for negativa e a derivada em um ponto posterior for positiva, estamos trabalhando com um ponto de mínimo.

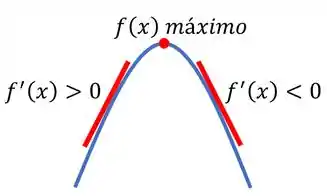
Para saber se o ponto crítico é um ponto de máximo, fazemos o mesmo, porém se a derivada em um ponto anterior ao nosso ponto for positiva e a derivada em um ponto posterior for negativa, estamos trabalhando com um ponto de máximo.

O ponto de sela irá ocorrer quando as derivas dos pontos próximos tiverem o mesmo sinal.

E assim respondemos mais uma questão. Bora olhar a próxima!