UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Rubens Sucupira - Lista 3, Questão 63
Deseja-se fazer um cartaz usando uma folha de papel retangular de de área. As margens no topo e na base devem medir e nos lados, . Determine as dimensões dessa folha, sabendo que a área impressa é máxima.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar as dimensões máximas da folha de área , que vai ser usada pra fazer um cartaz de margens superior/inferior igual e lateral de .
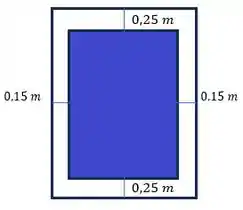
Se e são as medidas superior/inferior e lateral da folha, então nossa área será dada por:
E se e são, respectivamente, as medidas superior/inferior e lateral da folha, considerando as margens, então temos:
Dessa forma, considerando as margens, nossa área será dada pelo produto de por . Dessa expressão, nós vamos calcular a área máxima, derivando e igualando o resultado a zero para obter o valor das dimensões.
Vamos lá!
Passo 2
Vamos começar escrevendo a expressão da nossa área, considerando as margens:
Como , temos . E substituindo, ficamos com:
Passo 3
Derivando essa expressão, temos:
Igualando a zero pra encontrar os pontos críticos da função:
Isolando , temos uma das nossa dimensões:
Substituindo em , temos:
E encontramos as dimensões da nossa folha.
Valeu, galera! Até a próxima! 😉