Uma determinada máquina deve operar em velocidade constante de rotação. Sua jornada de trabalho é limitada entre rotações por minuto. O custo energético da máquina, medido por , é de por minuto e é consumido em uma razão de por minuto. O operador da máquina é pago a um custo de reais por minuto. Considere que a velocidade de rotação constante é obtida logo que a máquina entre em funcionamento. Determine para cada valor de , a velocidade de rotação que se obtém o custo mínimo consumido pela máquina em uma jornada de trabalho, sabendo que
Passo 1
Falaaa, pessoal! A primeira coisa que pega nessa questão é o português. Nós, na nossa casinha, pagamos conta de luz em que é uma unidade de energia, então vamos supor que os reais sejam o preço do , de forma que a nossa taxa constante de consumo energético ao longo de um dia seja:
Como e são constantes ao longo de uma jornada de trabalho a taxa será constante e o custo mínimo será consequência de uma taxa mínima.
Passo 2
Analisemos a taxa quanto ao mínimo. Em primeiro lugar, observe que a taxa é uma parábola de concavidade para cima cujo eixo de simetria é o eixo y e com vértice em :
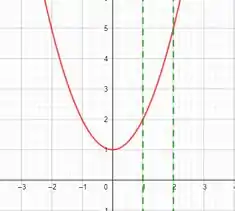
A menor taxa para um intervalo , e para todo obviamente será em , uma vez que o ramo positivo da parábola é estritamente crescente.
Resposta