UnB, Sem Campus, Cálculo 2, P2 - 2008.2, Questão 2
Determinar os pontos dos extremos relativos e os pontos de curvatura máxima da curva
De qual lado dos extremos relativos encontram-se os pontos de curvatura máxima? Qual é o valor da curvatura máxima? Compare-o com o valor da curvatura nos extremos relativos.
(Sugestão: Esboçar a curva aproximadamente!)
Passo 1
Eaee!!! Belezinha? Bom... Para determinar os pontos de extremos relativos e os pontos de curvatura máxima da curva , precisamos calcular as derivadas primeira e segunda da função e analisar os seus valores.
Dessa forma, temos as derivadas:
E
Agora, precisamos descobrir os pontos críticos para podermos prosseguir em busca da curvatura máxima!
Bora lá??!!
😉
Passo 2
Assim, vamos encontrar os pontos críticos igualando a derivada primeira a zero e resolvendo a equação:
Portanto, os pontos críticos são e .
Passo 3
Agora, podemos analisar os pontos críticos e a curvatura da curva.
- Ponto :
- Ponto :
Substituindo na equação original, temos:
Portanto, o ponto é um extremo relativo.
Substituindo na segunda derivada, temos:
Portanto, a curvatura neste ponto é .
Substituindo na equação original, temos:
Portanto, o ponto é outro extremo relativo.
Substituindo na segunda derivada, temos:
Portanto, a curvatura neste ponto é .
Agora, podemos comparar as curvaturas nos pontos de extremos relativos e nos pontos de curvatura máxima
Passo 4
No ponto , a curvatura é , enquanto no ponto , a curvatura é .
Portanto, a curvatura é máxima no ponto .
Os pontos de curvatura máxima estão localizados do lado oposto dos pontos de extremos relativos.
No caso desta curva, o ponto de curvatura máxima está à direita do ponto .
Passo 5
Utilizando um software de simulação numérica, podemos plotar o gráfico e analisar os pontos que descobrimos:
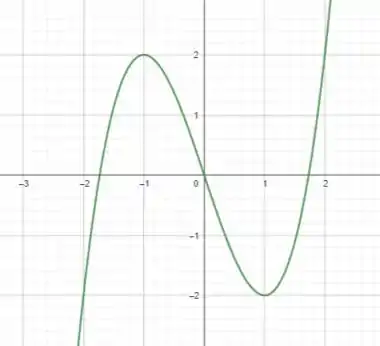
Entendeu direitinho? Responde aee ;)
Resposta
Ei, a resposta está no passo a passo :)