Determine as dimensões do cilindro circular reto de maior volume possível que esteja inscrito em um cone circular reto de volume fixo.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar as dimensões máximas do cilindro reto que tá inscrito em um cone de volume fixo. Vamos supor que sejam e a altura e o raio fixos do cone, respectivamente. E que sejam e , o raio e a altura variáveis do cilindro, respectivamente.
Assim, fazendo um corte nesse cone, temos a figura abaixo:
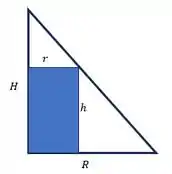
O triângulo menor de cima é semelhante ao triângulo maior, então podemos usar as relações de semelhança de triângulo para encontrar uma expressão para o raio do cilindro. Além disso, nós sabemos que o volume do cilindro por:
Assim, vamos encontrar uma expressão para a área , derivar essa expressão e igualar o resultado a zero para encontrar seus candidatos a máximo.
Vamos lá!
Passo 2
Usando a semelhança de triângulos, temos:
Isolando , temos o raio do cilindro dado por:
Passo 3
Como o volume do cilindro é , substituindo , temos:
E a altura do cilindro vai de zero até a altura do cone, então essa relação é válida para . Agora derivando a expressão que encontramos, vamos obter:
Igualando essa derivada a zero, vamos encontrar os pontos críticos da função:
Isolando a , temos:
Passo 4
Agora vamos ver se é um ponto de mínimo ou de máximo. Fazemos isso usando o teste da segunda derivada. Assim, derivando , temos:
Substituindo :
Como , pelo teste da segunda derivada, esse é realmente um ponto de máximo da função.
Passo 5
Agora que já descobrimos a altura máxima, vamos substituir na expressão do raio, para encontrar o raio máximo do cilindro:
Valeu, galera! Até a próxima! 😉