UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Rubens Sucupira - Lista 3, Questão 67
Determine as dimensões do cone circular reto de volume mínimo que pode ser circunscrito a uma esfera de de raio.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar as dimensões mínimas do cone circular reto que pode tá dentro de uma esfera de raio . Em corte, seria isso aqui:
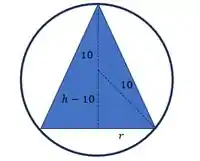
Daí, pelo teorema de Pitágoras, no triângulo retângulo que apareceu ali embaixo, temos:
Então, nós vamos isolar nessa equação e substituir a expressão encontrada na fórmula do volume do cone:
Assim, vamos ter em função de . Para descobrir os pontos críticos dessa função, vamos derivar e igualar a zero. E usar o teste da segunda derivada para descobrir se os pontos críticos encontrados são pontos de máximo ou de mínimo.
Vamos lá!
Passo 2
Encontrando uma expressão para na equação:
Temos:
Substituindo na expressão do volume, , temos:
Passo 3
Agora vamos derivar e igualar a zero para encontrar os pontos críticos. Derivando em relação a , temos:
Igualando a zero:
Então, pra que esse produto seja verdadeiro, temos:
ou
Esses são nossos pontos críticos.
Passo 4
Derivando mais uma vez, vamos descobrir se esses pontos são de máximo ou mínimo.
Substituindo :
E substituindo :
Como , temos um ponto de máximo, pelo teste da segunda derivada. E como , temos um ponto de mínimo, também pelo teste da segunda derivada. Como a questão quer saber as dimensões mínimas do cone, seria:
E consequentemente,
O que é meio óbvio, porque a circunferência não limita as dimensões do cone inferiormente. Talvez a intenção da pergunta fosse saber as dimensões máximas do cone. Nesse caso, usaríamos o mesmo procedimento, só que o nosso resultado seria .
Valeu, galera! Até a próxima! 😉