UFSC, Joinvile, Cálculo II, Provas Profº Rómulo Castillo - P2 2015.1, Questão 3
Determine os máximos e mı́nimos de na região definida no conjunto
Passo 1
Eaew, belezinha?
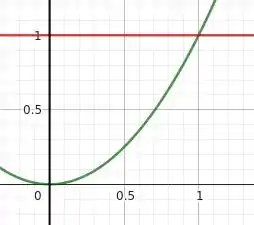
A questão pede para a gente determinar os máximos e mínimos de uma função de duas variáveis em uma região R do plano xy, definida pelas curvas , , para . A figura abaixo ilustra essas curvas em vermelho, verde e preto, respectivamente, delimitando a região R do plano onde queremos determinar os máximos e mínimos.
Bem, a gente sabe que, em pontos de extremo de uma função, suas derivadas são nulas. Então calcular as derivadas parciais da função é crucial para a determinação dos extremos. No entanto, em uma região fechada e limitada, a função pode ter seus extremos nos limites da região. Nesse caso, a gente também precisa verificar a função nos limites da região R e comparar com os extremos obtidos através da derivação. Então, primeiro vamos lá calcular as derivadas parciais da função!
Passo 2
Primeiro, vamos calcular a derivada de f em relação a x. Para calcular essa derivada parcial, consideramos a variável y como constante. Assim, obtemos
Em um ponto de extremo, a derivada deve ser nula. Então, dessa derivada parcial obtemos
Semelhantemente, calculando a derivada de f em relação à y, mantendo x constante, obtemos
Novamente, em um ponto de extremo, a derivada deve ser nula. Então, dessa derivada parcial obtemos
Juntando as duas equações, obtemos que
Essa equação possui soluções y = 0 e y = -1, que corresponde então aos pontos (0,0) e (1,-1) do plano xy. Contudo onde apenas o ponto (0,0) pertence à região R. Nesse ponto a função é nula: f(0,0) = 0. Agora precisamos verificar os valores da função nas bordas do intervalo para ver se existem valores menores ou maiores que f(0,0). Então vamos lá!
Passo 3
Primeiro, vamos começar com a borda representada pelo segmento d reta y = 1, (curva vermelha na figura). A interseção do plano y = 1 com a função f(x,y) é a curva
Que é uma função que possui valor máximo em x = 0, quando ela assume o valor igual à 1 e possui seu valor mínimo em x = 1, quando ela vale -3. Ok, vamos guardar esses valores e prosseguir para a próxima curva da região R: x = 0, (curva preta na figura). A interseção do plano x = 0 com a função f(x,y) é dada pela função
Como y está sempre entre 0 e 1, os valores máximos e mínimos que essa função assume são, respectivamente, 1 e 0. Vamos guardar também esses valores em mente e seguir para a última curva da região R: (curva verde na figura). A interseção dessa superfície com a função f(x,y) define a função
Como x está sempre entre 0 e 1, temos que os valores máximo e mínimo dessa função são, respectivamente, 0 e -3.
Então, temos que, de todos os valores que obtivemos, o menor é -3 (que ocorre quando x = 1 e, consequentemente, y = 1) e que o maior valor, que é igual a 1, ocorre quando x = 0 e y = 1.
Como -3 é menor que 0 (valor obtido da função em um ponto com derivada nula) e como 1 é maior que o valor obtido através da derivada nula, temos que os pontos de máximo e mínimo a função se encontram na borda do intervalo, nos pontos (0,1) e (1,1), respectivamente, com valores 1 e -3, e não no ponto de extremização da função.
Resposta
Máximo = 1, em (0,1)
Mínimo = -3, em (1,1)