UNICAMP – Cálculo 2 – Provas antigas – P2 – 2022.1 – 1b
Determine os pontos de máximo e mínimo da função restrita à elipse . Determine os valores máximos e mínimos.
Passo 1
Fala, meus lindos e lindas 😊, tudo certinho com vocês? Bora pra questão sem pena. Do item passado, a gente já tem os pontos de máximo e mínimo da função. Sabe quais são? Eles são justamente:
E por definição vem a mágica. Por definição de pontos máximos e mínimos, sabemos que qualquer função tal que:
É uma função de máximo ou mínimo, dependendo se o ponto for um ponto de máximo ou mínimo.
Passo 2
Dessa forma, pro nosso que ponto de máximo, a função que determina o valor máximo é:
Analogamente, para :
Que por sua vez é ponto de mínima. Assim, nossa figura fica:
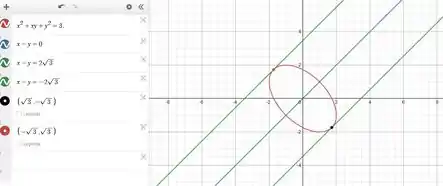
E é isso turminha! Finalizamos por aqui 😊. Se ainda restou alguma dúvida, ou gostaria de relatar alguma coisa, manda um feedback pra gente! Vamos adorar te responder, vai se rapidinho