2. Encontre os valores máximo e mínimo locais e globais de no intervalo.
g.
Passo 1
Oi, galerinha! Tudo bom? Antes de tudo, precisamos entender que pontos são esses!
Um ponto de máximo é um ponto na função que é maior que os pontos próximos a ele. Em um gráfico, é como se tivéssemos o topo de uma colina. Já um ponto de mínimo é justamente o contrario, podemos pensar que ele tem a forma de um buraco.
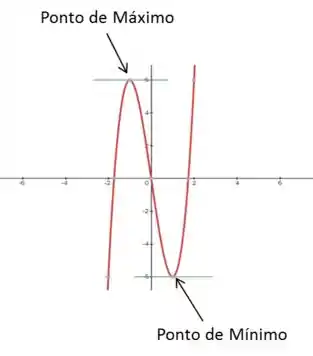
E como sabemos se uma função não terá um máximo ou mínimo?
Repara que no gráfico acima possui uma reta azul, nos pontos de máximo e mínimo, que representa a reta tangente ao ponto. Se a gente olhar com calma, vamos perceber que tanto pra pontos de máximo quanto pra pontos de mínimo a reta tangente à eles é horizontal, ou seja, o coeficiente angular delas é zero.
Lembra que o coeficiente angular da reta tangente a um ponto é justamente a derivada da curva naquele ponto? Opaaa, então a gente acabou de chegar a conclusão de que para pontos de máximo e mínimo, a derivada da curva é nula naquele ponto.
Ou seja, galerinha, o que temos que fazer aqui é derivar e igualar a zero para acharmos os pontos de máximo e mínimo.
Bora lá!
Passo 2
Temos a seguinte função,
Derivando ficamos com,
Igualando a zero ficamos com,
Note que este valor está dentro do intervalo dado
Agora temos que descobrir quais pontos são máximo e mínimos. Para isso, vamos fazer o teste da segunda derivada!
Passo 3
Neste teste nós temos que calcular a segunda derivada e substituir o nosso ponto, no caso . Se a derivada segunda for maior que zero temos um ponto de mínimo e se ela for menor que zero temos um ponto de máximo.
Fazendo a segunda derivada ficamos com,
Note que a segunda derivada deu uma constante igual a . Ou seja, ela é maior que zero, então temos um ponto de mínimo.
Resposta
Ponto de mínimo em