UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.11
Esboce o gráfico de , com . Quais são os valores máximos e mínimos globais desta função?
Passo 1
Eaee!!! Belezinha? Bom... para esboçar o gráfico de , com primeiramente precisamos encontrar os valores críticos, onde a derivada da função é igual a zero.
Em seguida, determinamos os pontos de inflexão e analisamos o comportamento da função nos extremos do intervalo.
Com isso, encontraremos os valores máximos e mínimos globais desta função.
Agora vamos lá aplicar!!
😉
Passo 2
Sabemos que a derivada da função é dada por:
Para encontrar os valores críticos, igualamos a derivada a zero:
ou
Passo 3
Agora, vamos calcular os valores de correspondentes:
E
Assim, os pontos e são os valores onde a derivada irá mudar de sinal.
A partir disso, plotando os pontos, temos:
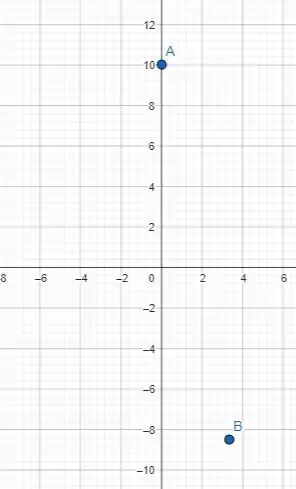
Passo 4
Assim, levando em conta que estamos estudando uma função cúbica e que o sinal que acompanha é positivo, então temos o seguinte gráfico:
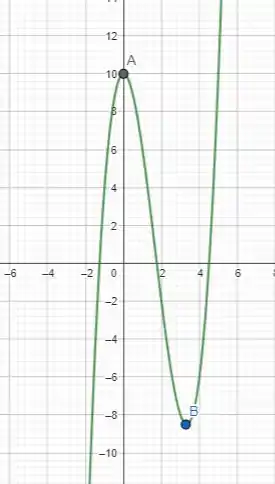
Assim, para o intervalo temos que o máximo global é o ponto e o mínimo global é o ponto .
Entendeu direitinho? Responde aee ;)
Resposta
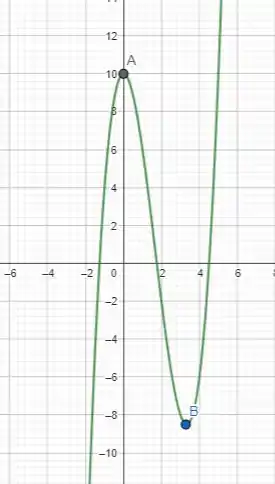
Máximo e mínimo globais em e