UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.3.2c
2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(c)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema foi dado uma função e nosso objetivo é esboçar o gráfico de , o domínio, as assíntotas, os intervalos de crescimento e decrescimento, os extremos relativos e absolutos, os intervalos onde a função tem concavidade positiva e negativa e também os pontos de inflexão.
Pouca coisa, né? Graças a Deus! Tem ideia de como fazer tudo isso? 😐
O domínio da função é nada mais que os possíveis valores que pode assumir em para que seja definida.
Para calcular as assíntotas, fazemos o limite de para e , se os resultados forem iguais, temos uma assíntota horizontal em . Agora para as assíntotas verticais fazemos o limite de para tendendo ao ponto onde é indefinido.
Já a partir da derivada de , podemos obter os intervalos onde é crescente e decrescente . Também fazendo podemos obter os pontos críticos onde podemos descobrir quais são de máximo, de mínimo ou de inflexão.
Muita coisa, não é? Bora começar! 👀
Passo 2
A função dada é
Perceba que a função se trada de uma fração onde no numerador temos e no denominador .
No numerador não temos restrição alguma pra , porém no denominador de qualquer fração sabemos que não podemos ter , logo, para nossa função temos que
Dessa forma, o domínio de é dado por
Agora para verificar a existência de assíntotas horizontais, fazemos
Se aplicarmos diretamente, vamos cair em uma indeterminação , então podemos aplicar a regra de L’Hopital e derivar o numerador e o denominador...
Dessa forma, temos um número relativamente pequeno sendo dividido por um número muito grande, ou seja, o resultado tende a
Já para assíntotas verticais temos
Quando tende a , o numerador tende a um número muito pequeno, muito próximo de , assim quando temos um número relativamente grande sendo dividido por um número muito pequeno o resultado é um número tão grande que se aproxima de , assim, podemos dizer que
Dessa forma, em e em temos assíntotas verticais!
Logo, em temos uma assíntota horizontal e assíntotas verticais em e ...
Tranquilo até aqui? 😉
Passo 3
Agora vamos calcular a derivada de para determinar os outros resultados.
Pela regra do quociente, temos
A partir dessa derivada, podemos determinar os intervalos de crescimento e decrescimento de , os extremos relativos, os pontos críticos e os intervalos de concavidade de .
Fazendo , encontramos os pontos críticos, como
Simplificando...
Perceba que não é possível elevar um número ao quadrado (dentro dos números reais) e resultar um número negativo.
Dessa forma, não temos pontos de máximos, mínimos e nem pontos de inflexão já que não temos pontos críticos...
Legal, né? 😐
Passo 4
A partir dessas informações que obtemos até agora, podemos afirmar que em a função é crescente.
Com isso, temos muitas informações para esboçar o gráfico da função como...
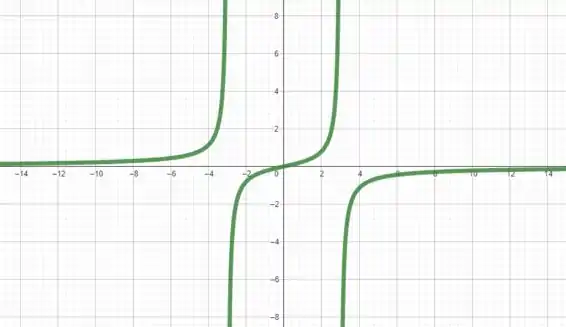
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Em temos uma assíntota horizontal e assíntotas verticais em e .
não possui pontos críticos.
a função é crescente.