Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Máximos e Mínimos

Ver Teoria
Exercício 355123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 7 - Máximos e Mínimos, Questão 1.1b

1.1. Esboce a região D e determine o máximo e o mínimo absolutos da função f : D → R quando

b. f x , y = x y e - x 2 - y 2 e D = x , y ∈ R 2 : x 2 + y 2 ≤ 2 ,   x ≤ 0 , y ≥ 0 ;

Passo 1

Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema queremos obter os pontos máximos e mínimos da função f x , y = x y e - x 2 - y 2 dentro da região D limitada pelo semicírculo x 2 + y 2 ≤ 2 em que x ≤ 0 e y ≥ 0 .

Parece de boa? 👀

Nesses casos, quando temos que obter os pontos máximos e mínimos podemos seguir uns passos...

Primeiro calculamos os pontos críticos de f normalmente e verificamos se esses pontos estão dentro da região D ... caso eles não estiverem, descartamos.

Depois calculamos os pontos críticos nas bordas da região substituindo as equações que limitam D na função f .

Sacou? Bora começar! 😉

Passo 2

Primeiro vamos obter a região D

Esboçando o setor circular dado por x 2 + y 2 ≤ 2 em que x ≤ 0 e y ≥ 0 , temos

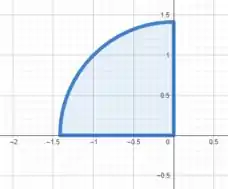
Obtendo os pontos críticos da função f para x , temos

f x = 0

∂ x y e - x 2 - y 2 ∂ x = 0

Pela regra do produto e da cadeia...

y e - x 2 - y 2 - 2 y x 2 e - x 2 - y 2 = 0

y e - x 2 - y 2 = 2 y x 2 e - x 2 - y 2

1 = 2 x 2

x = ± 1 2

Fazendo o mesmo agora para y ...

f y = 0

∂ x y e - x 2 - y 2 ∂ y = 0

x e - x 2 - y 2 - 2 x y 2 e - x 2 - y 2 = 0

x e - x 2 - y 2 = 2 x y 2 e - x 2 - y 2

1 = 2 y 2

y = ± 1 2

Tranquilo até aqui? 😬

Passo 3

Até agora encontramos quatro pontos que são críticos, mas quais deles estão dentro da região D ?

A região D é definida em x ≤ 0 e y ≥ 0 , ou seja, temos um único ponto dentro dos que encontramos que satisfaz esses critérios.

P 1 = - 1 2 , 1 2

A próxima análise que temos que fazer é nas curvas que limitam a região D , ou seja, x = 0 , y = 0 e y = 2 - x 2 .

Para x = 0 ...

f 0 , y = 0 y e - 0 2 - y 2 = 0

Para y = 0 ...

f x , 0 = x 0 e - x 2 - 0 2 = 0

Nesses casos, a função é constante e igual a 0

Agora para y = 2 - x 2

f x , 2 - x 2 = x 2 - x 2 e - x 2 - 2 - x 2 2

f x = x 2 - x 2 e - x 2 - 2 + x 2

f x = x 2 - x 2 e - 2

Obtendo os pontos críticos dessa função, temos

f x = ∂ x 2 - x 2 e - 2 ∂ x = 0

1 e 2 2 - 2 x 2 2 - x 2 = 0

x = ± 1

Mas como x ≤ 0 , então o ponto crítico nesse caso é dado por

P 2 = - 1,1

Bacana, não é? 😐

Passo 4

Por fim, vamos comparar a imagem de f nos pontos encontrados e nos vértices 2 , 0 , 0 , 2 e 0,0 .

Primeiro vamos obter f P 1 , P 1 = - 1 2 , 1 2

x y e - x 2 - y 2

f - 1 2 , 1 2 = - 1 2 1 2 e - - 1 2 2 - 1 2 2 = - 1 2 e - 1 2 - 1 2

f - 1 2 , 1 2 = - 1 2 e

Para P 2 = - 1,1

f - 1 , 1 = - 1 1 e - - 1 2 - 1 2

f - 1,1 = - 1 e 2

Para os vértices 2 , 0 ,   0 , 2   e   0,0 . Já sabemos que f é 0 pois estão sob a reta x = 0 e/ou y = 0 ...

Portanto o máximo de f em D é obtida em 2 , 0 ,   0 , 2   e   0,0 onde f = 0

E o mínimo é obtido é P 1 = - 1 2 , 1 2 em que f = - 1 2 e

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

O máximo de f em D é obtida em 2 , 0 ,   0 , 2   e   0,0 onde f = 0 e o mínimo é obtido é P 1 = - 1 2 , 1 2 em que f = - 1 2 e

Exercícios de Livros Relacionados

O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 ⁡ x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)