1.1. Esboce a região e determine o máximo e o mínimo absolutos da função quando
c. e ;
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema queremos obter os pontos máximos e mínimos da função dentro da região limitada pela hipérbole em .
Parece de boa? 👀
Nesses casos, quando temos que obter os pontos máximos e mínimos podemos seguir uns passos...
Primeiro calculamos os pontos críticos de normalmente e verificamos se esses pontos estão dentro da região ... caso eles não estiverem, descartamos.
Depois calculamos os pontos críticos nas bordas da região substituindo as equações que limitam na função .
Sacou? Bora começar! 😉
Passo 2
Primeiro vamos obter a região
Esboçando a região limitada por pela hipérbole entre e , temos
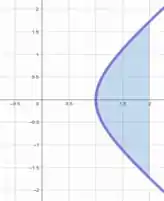
Primeiro vamos obter os pontos críticos gerais da função.
Portanto a função possui apenas um ponto crítico e é dado em , mas esse ponto está fora do intervalo de .
Agora vamos analisar a função nas curvas que limitam a região , primeiro na reta , temos
Como se trata de uma reta, não temos pontos críticos sobre ela...
Agora substituindo na função fazendo
Obtendo os pontos críticos dessa curva, temos
Como ambos os pontos estão fora do intervalo , então até aqui não temos nenhum ponto a se analisar...
Tranquilo até aqui? 😉
Passo 3
Dessa forma, só nos resta obter as imagens de nos vértices e
Para o ponto
Para o ponto
Com isso vemos que o ponto máximo é com e o ponto mínimo é com
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
O ponto máximo é com e o ponto mínimo é com .