USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 7 - Máximos e Mínimos, Questão 1.1a
1.1. Esboce a região e determine o máximo e o mínimo absolutos da função quando
a. e é o triângulo (com interior e lados inclusos) cujos vértices são , e ;
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema queremos obter os pontos máximos e mínimos da função dentro da região limitada pelo triangulo de vértices em , e .
Parece de boa? 👀
Nesses casos, quando temos que obter os pontos máximos e mínimos podemos seguir uns passos...
Primeiro calculamos os pontos críticos de normalmente e verificamos se esses pontos estão dentro da região ... caso eles não estiverem, descartamos.
Depois calculamos os pontos críticos nas bordas da região substituindo as equações que limitam na função .
Sacou? Bora começar! 😉
Passo 2
Primeiro vamos obter a região
Esboçando os vértices e as retas que ligam os vértices, temos
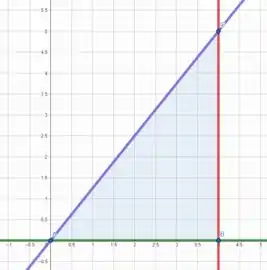
Com isso, vemos que as bordas da região é dada pelas curvas , e .
Vamos começar obtendo os pontos críticos da função , ou seja
Obtendo as derivadas parciais...
Como o resultado é impossível, vemos que não possui pontos críticos, logo podemos restringir a busca pelos pontos máximos e mínimos aos vértices de já que é um plano...
Para o ponto
Para o ponto
E para o ponto
Assim, vemos que o máximo de é dado no ponto onde .
Já o ponto mínimo é dado no ponto em que
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
Máximo:
Mínimo: